Additionneur binaire
Bonjour à toutes et à tous 😀
Additionner deux nombres c'est quelque chose d'assez simple, on l'apprend dès le CP. Soit on le fait de tête, soit sur ses doigts soit on pose l'addition sur papier.
Jusqu'à ce que les nombres soient trop grands ou que l'on ait la flemme de faire le calcul, on prend la calculette qui fait l'opération à notre place.
Mais vous vous êtes jamais demandé comment elle arrivait à faire le calcul ?
Moi si, et comme d'habitude on va aller beaucoup trop loin. 😅
Addition binaire
Avant d'automatiser il faut comprendre et analyser.
La première chose à savoir c'est qu'un nombre aussi simple que $2$ est déjà compliqué pour un ordinateur, ou plutôt il ne représente rien de physique.
C'est nous qui l'interprétons comme un $2$, la machine elle ne sait pas ce que c'est.
Pour lui permettre de comprendre nous devons parler sa langue, le binaire et représenter notre $2$ dans sa langue.
Ainsi notre addition
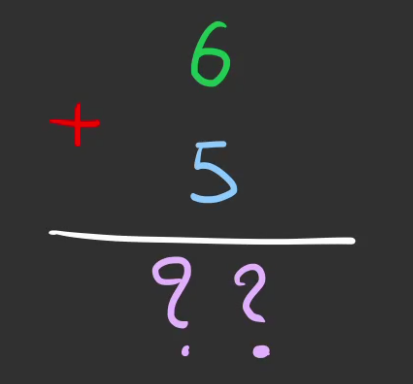
est représentée en binaire par
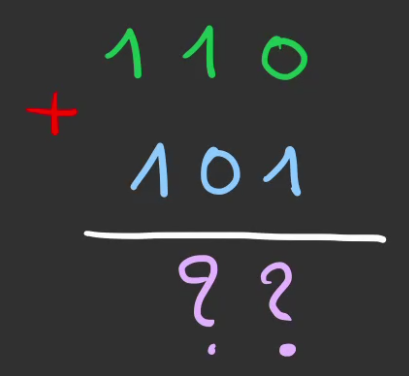
Les règles de l'addition en binaire sont comme suit

On remarque que $1 + 1 = 10$ et non $2$
On pose alors en suivant les règles de l'addition apprise au CP.
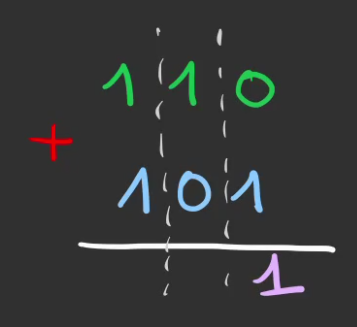
Jusqu'à arriver au cas où les deux éléments de la colonne sont des $1$.
On pose alors la retenu.
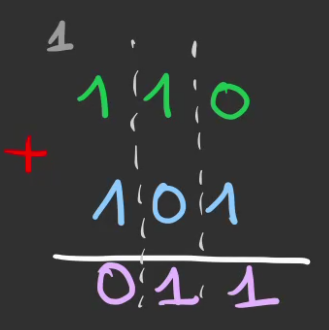
Que l'on fait redescendre dans le résultat.
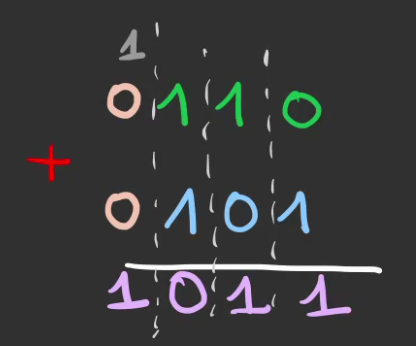
Si on fait la conversion de bases.
$$1011_{2} = 11_{10}$$
$X_n$ signifie $X$ en base $n$.
Donc $11_{10}$ veut dire $11$ en base $10$, notre base de tous les jours
Or $5 + 6 = 11$
On retombe sur nos pattes 😁
Table de vérité
Maintenant comment faire la même que l'on a fait mais avec un ordinateur.
D'abord, nous allons nous occuper de l'addition que d'une seule colonne.
Voici les différentes additions possible avec 1 bit.
$C$ pour carry en anglais ou "retenu".
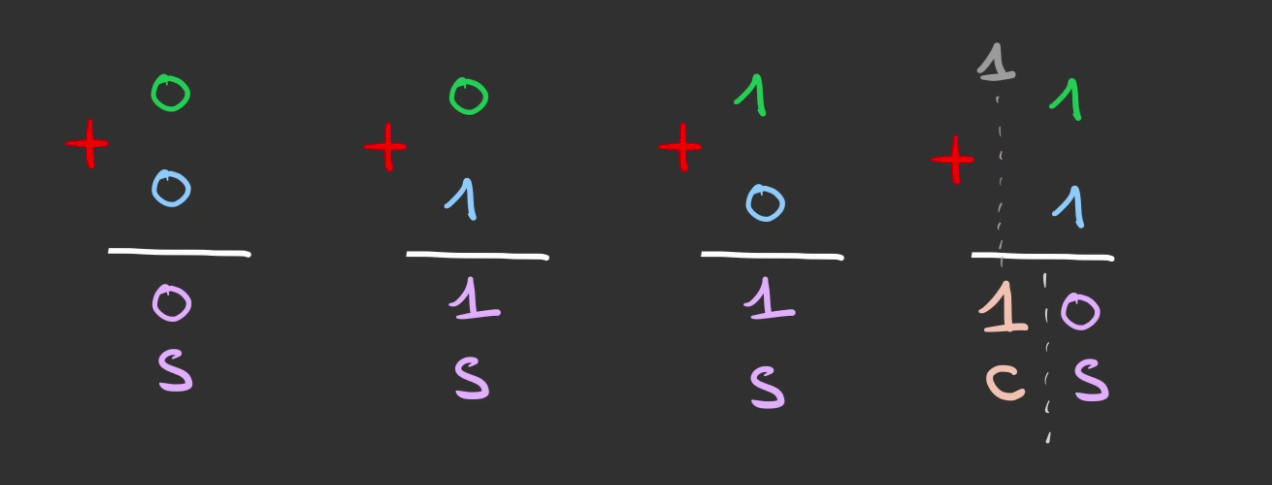
On regroupe ça dans un tableau que l'on nomme table de vérité.
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Nous allons d'abord déterminer lorsque l'addition vaut $1$
Deux cas émergent:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ce que nous dit le tableau est que pour avoir un $1$, il faut que $A = 1$ ou $B = 1$ mais pas les deux ensemble.
On appelle ceci un OU EXCLUSIF ou XOR.
Et on note $A \oplus B = S$
Le second élément que l'on désire obtenir est la retenu.
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ici, une seule manière d'obtenir un $1$ : $A =1$ et $B = 1$.
Il s'agit d'un ET Logique ou AND.
Et on note $ A \wedge B = C$
Portes logiques
Ok maintenant que l'on sait ce que l'on faire faire au système, il faut construire le câblage qui le réalise.
Transistor
On part de la base de l'electronique moderne: le transistor.
Il y a mille choses à en dire mais nous allons nous contenter du minimum syndical.
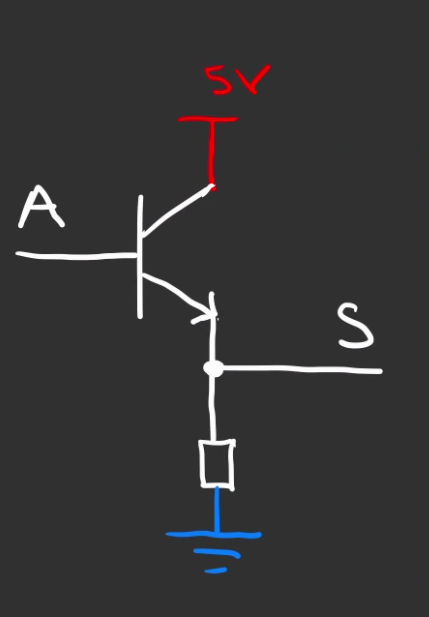
$A$ est l'entré et $S$ la sortie.
On applique du jus en "haut", on appelle ça un état logique "1". Ici signifié par le 5V rouge.
Et on met à la masse le bas séparé par une résistance pour que $S$ ne vaille pas 0 en permanence.
Lorsque $A = 0$, nous somme en état logique "0".
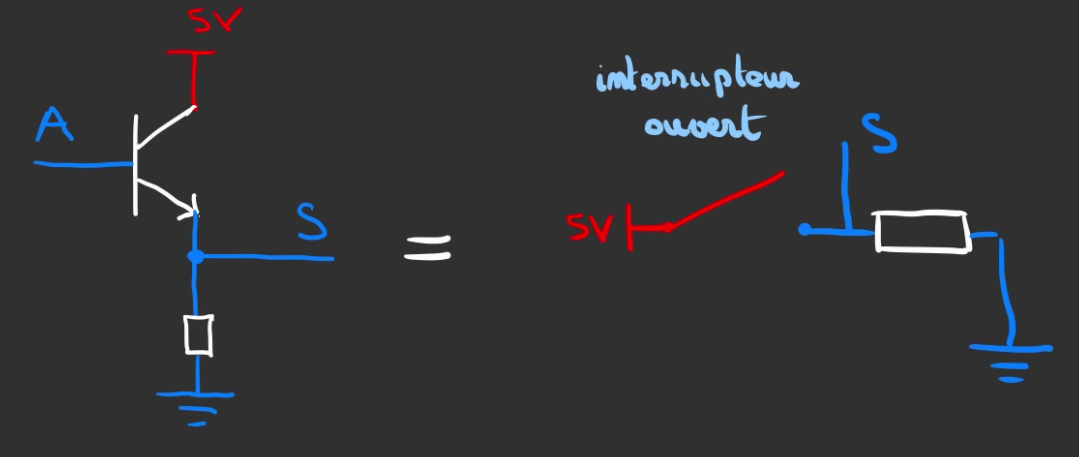
Le transistor est affilié à un fil ouvert. $S = 0$
Lorsque $A = 1$, nous somme en état logique "1".
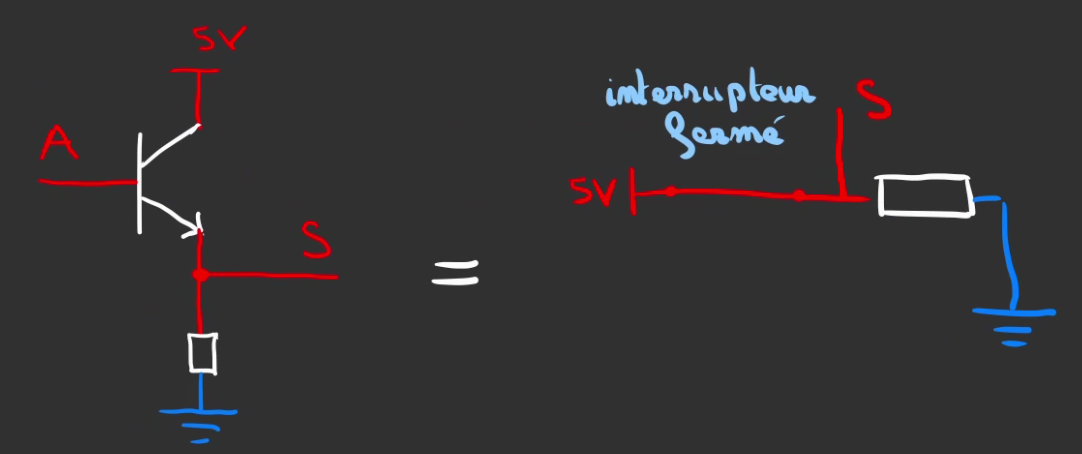
Le transistor est affilié à un fil ouvert. $S = 1$
Félicitation vous avez créé un fil !!!
Porte AND
Voyons pour rendre cela plus intéressant.
Si l'on prend 2 transistors nous pouvons construire quelque chose comme ceci.
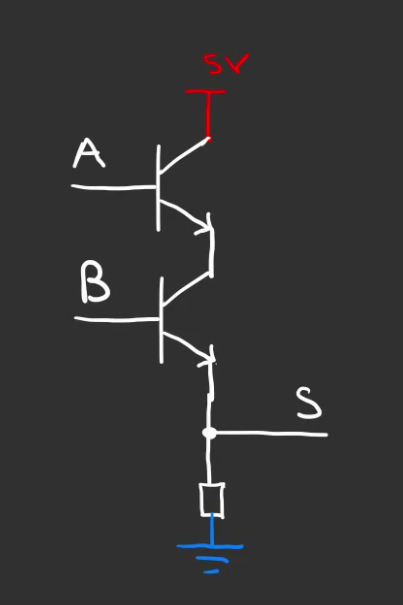
Si on joue avec les entrées
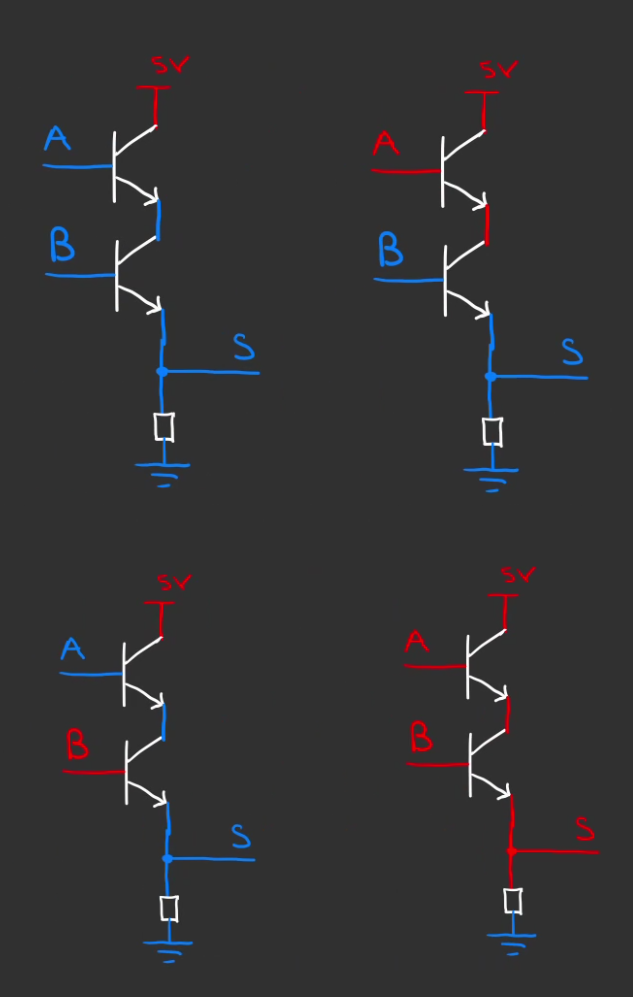
Nous avons bien quelque chose qui impose que les deux transistor soit passant pour que la sortie soit à "1".
On peut récapituler ça dans une table de vérité.
| A | B | $A \wedge B$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
On en fait une boîte qui a ce symbole.
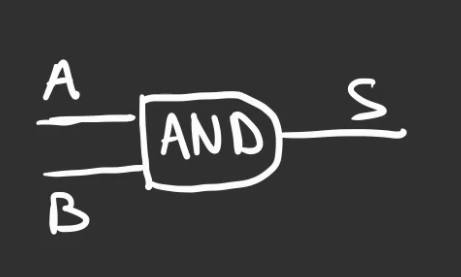
Porte NAND
On peut également inverser le résultat.
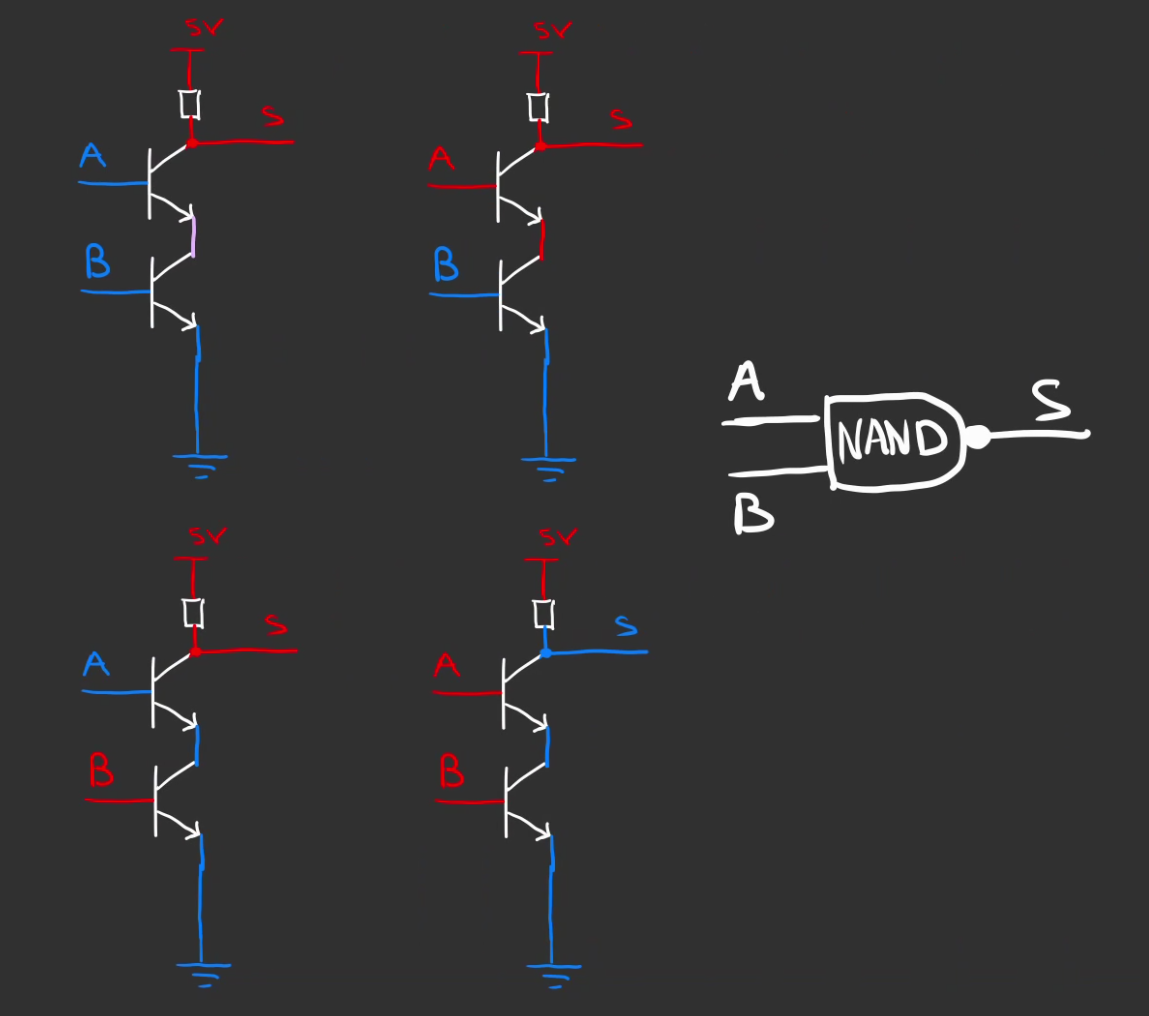
Remarquez le rond à la gauche du symbole, cela signifie que l'on inverse la sortie, le $0$ donne $1$ et inversement.
Dans les formules cette négation devient une barre horizontale.
| A | B | $\overline{A \wedge B}$ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Porte OR
Et également faire une alternative entre les entrées, l'une, l'autre ou les deux.
Voici le montage, ainsi que les variations de sorties en fonctions des entrées et le symbolce de la porte OR.
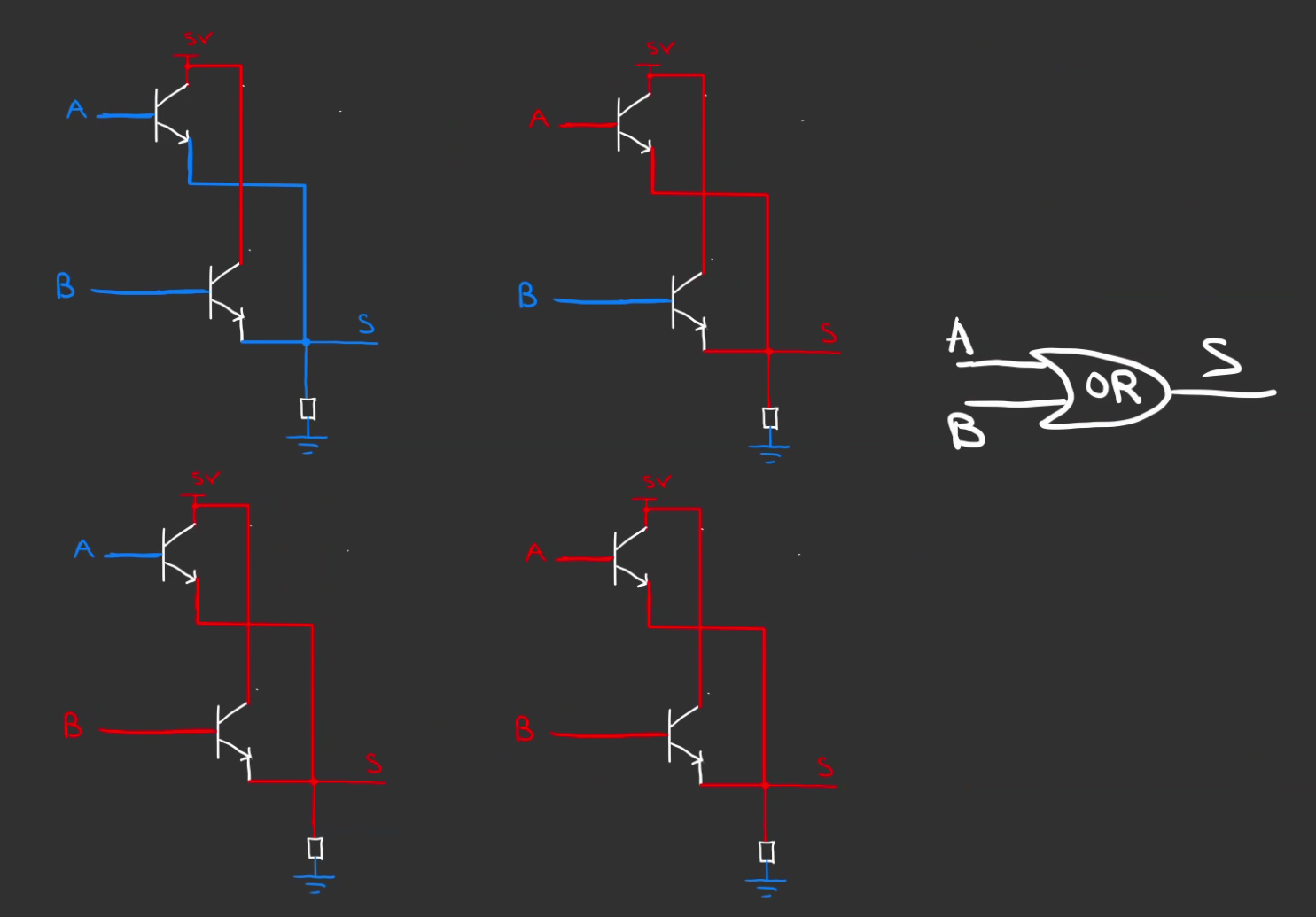
On note cette relation de OU : $S = A \vee B$
Et voici sa table de vérité.
| A | B | $A + B$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Porte XOR
Mais nous ce qu'on cherche c'est cette table ci:
| A | B | $S = A \oplus B$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Si on réfléchi un peu on peu écrire
$$ S = (A \wedge \overline{B}) \vee (\overline{A} \wedge B) $$
Autrement dit:
- $A = 1$ et $B = 0$
- $A = 0$ et $B = 1$
En bidouillant grâce à l'algèbre de Boole et la loi de De Morgan. On triche avec $$ X \wedge \overline{X} = 0 $$ Ce qui permet d'écrire $$ S = (A \wedge \overline{A}) \vee (A \wedge \overline{B}) \vee (\overline{A} \wedge B) \vee (B \wedge \overline{B}) $$ On utilise l'itentité remarquable qui nous donne $$S = (A \vee B) . (\overline{A} \vee \overline{B})$$ Par de De MorganAlgèbre de Boole
On finit par atterir sur:
$$S = (A \vee B) . (\overline{A \wedge B})$$
Que l'on cable en
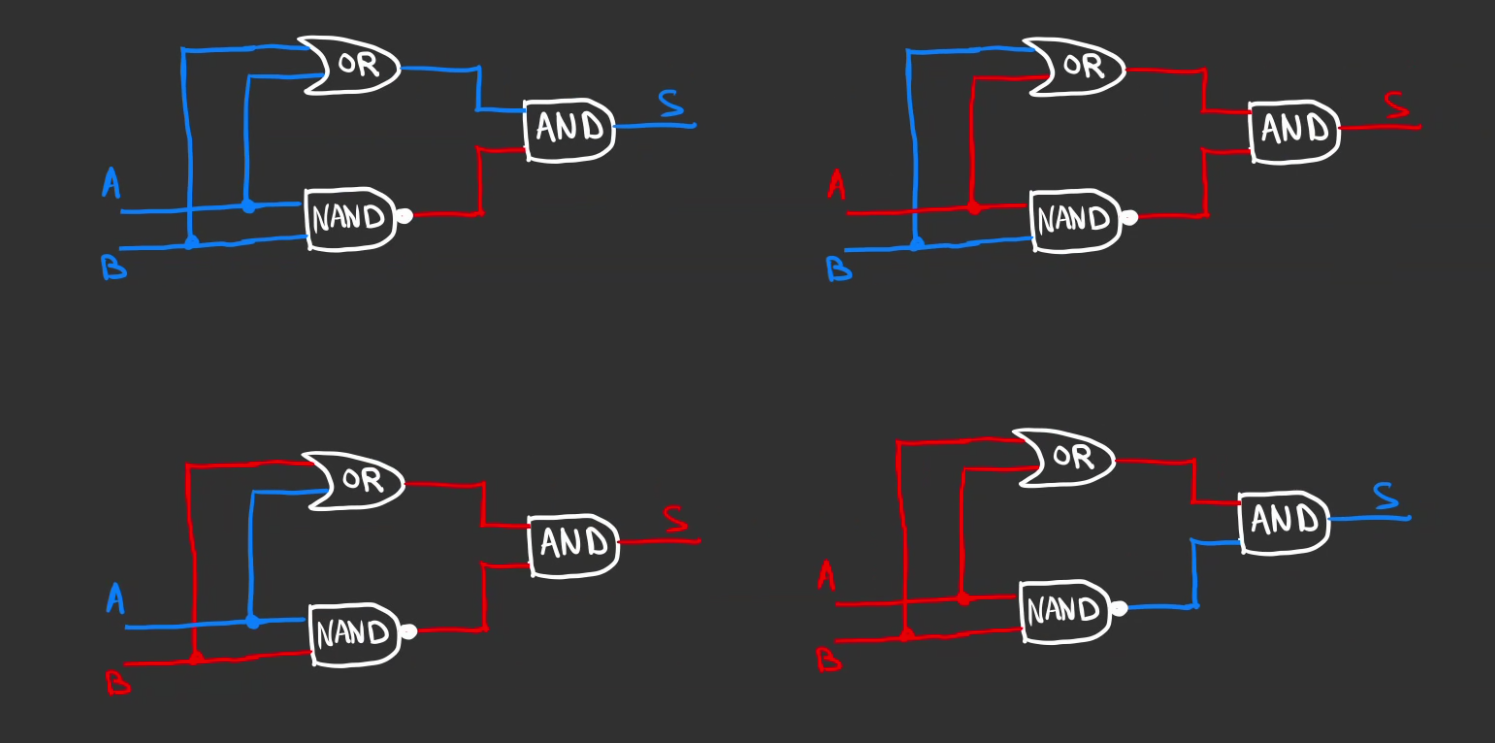
En faisant varier les entrées nous avons bien ce que l'on désire.
| A | B | $A \vee B$ | $\overline{A \wedge B}$ | $(A \vee B) \vee (\overline{A \wedge B}) = A \oplus B$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Voici son symbole:
Nous sommes ainsi capable de calculer la somme de deux bits ! 😁
Enfin presque il manque la retenu.
Mais comme $ C = A \wedge B$, la porte AND suffit. 🙂
Half Adder
Nous allons pouvoir construire ce que l'on nomme un demi-additionneur.
Son rôle est de calculer le résultat de l'addition et de l'éventuelle retenue.
Nous avons ainsi ces deux équations logiques:
$$\begin{cases} S = A \oplus B\space(somme)\\
C = A \wedge B \space (retenue) \end{cases} $$
Que l'on cable en:
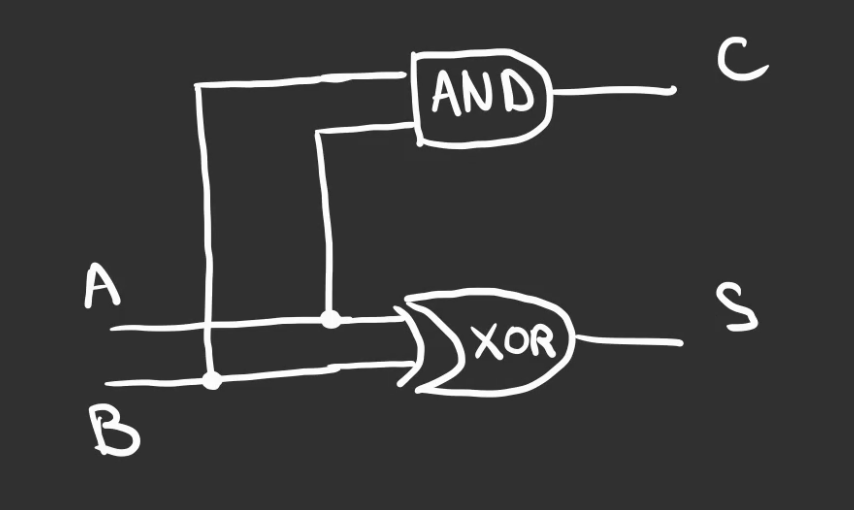
On enferme alors ce montage dans une boîte.
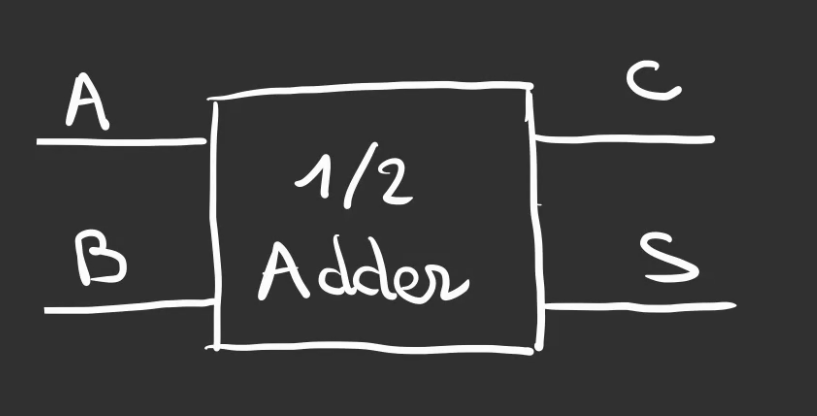
Que l'on peut alors alimenter pour voir son comportement
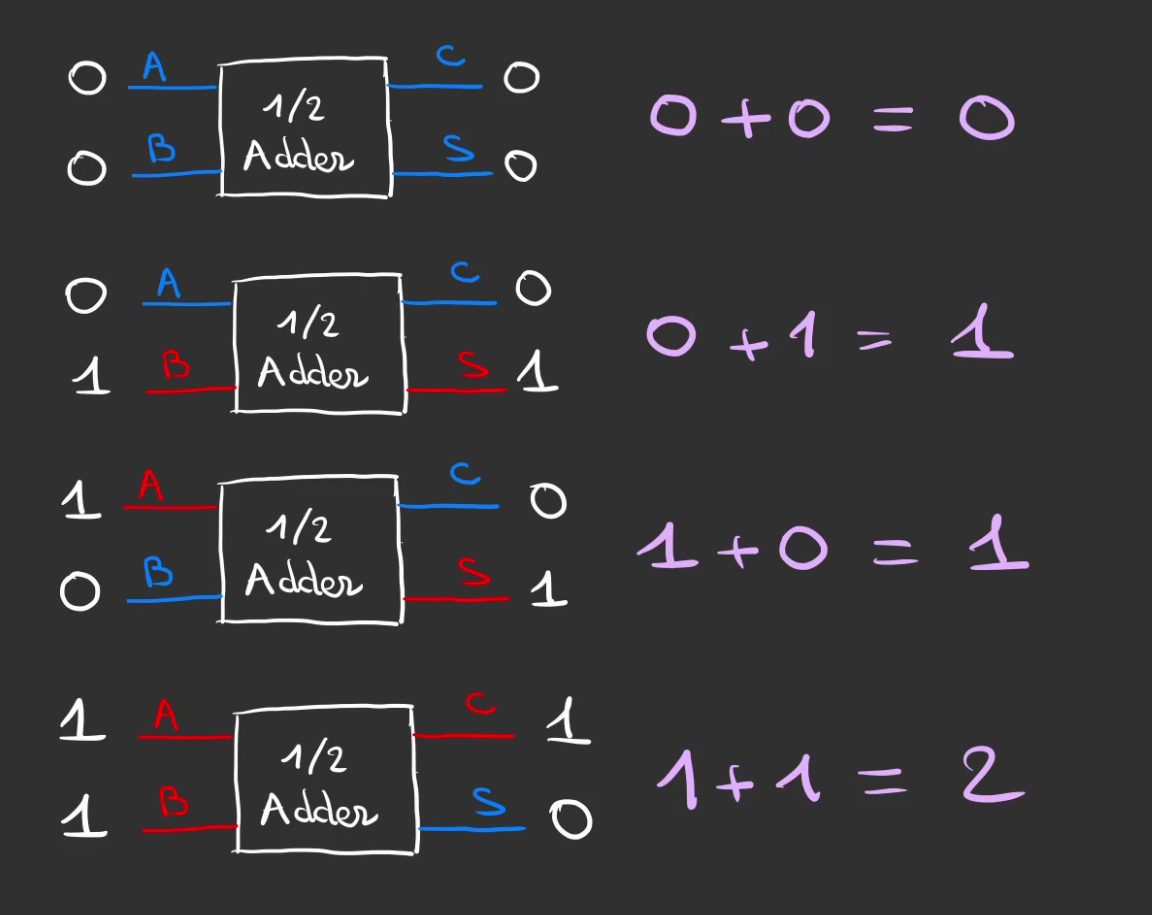
Cool ! 😎
Full Adder
Par contre on ne gère pas un des cas.
Lorsqu'une retenu vient d'une addition précédente.
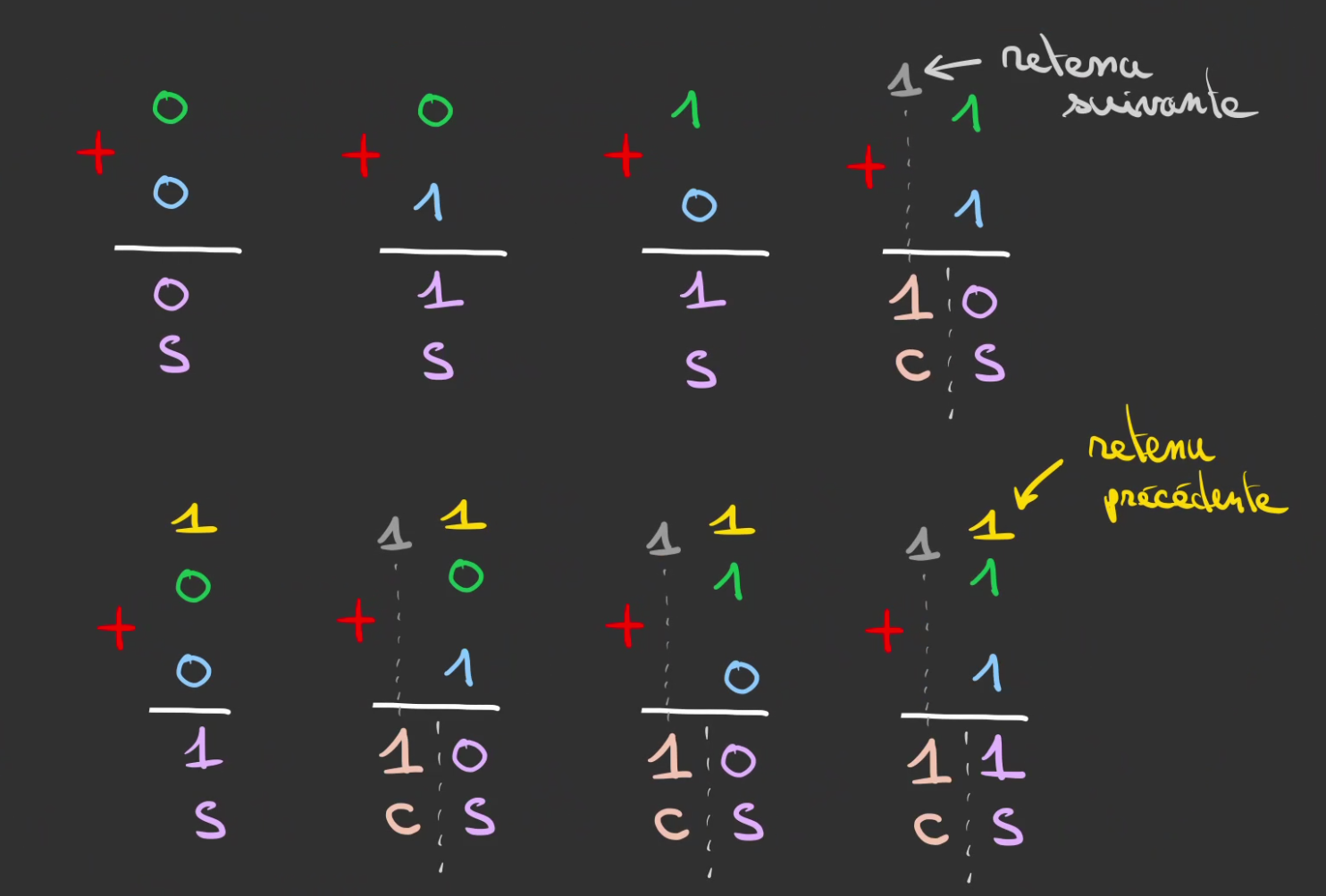
Notre nouvelle table de vérité devient
| $C_{in}$ | A | B | $C_{out}$ | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
On peut alors se dire que ce n'est qu'une addition de 3 nombres
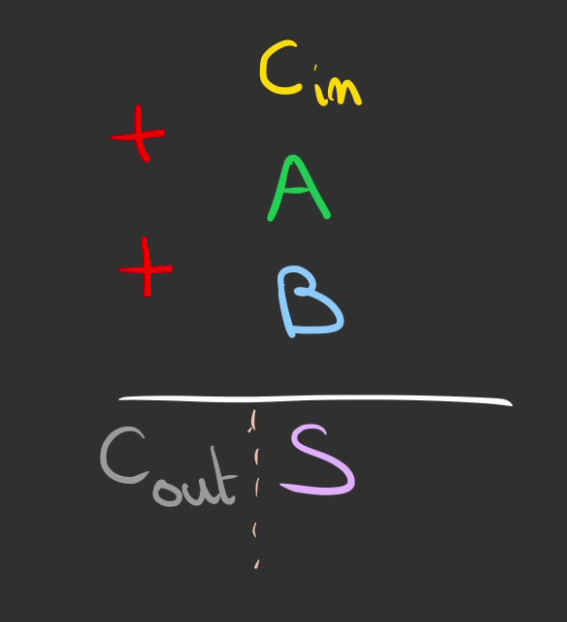
Que l'on casse en deux additions successives.
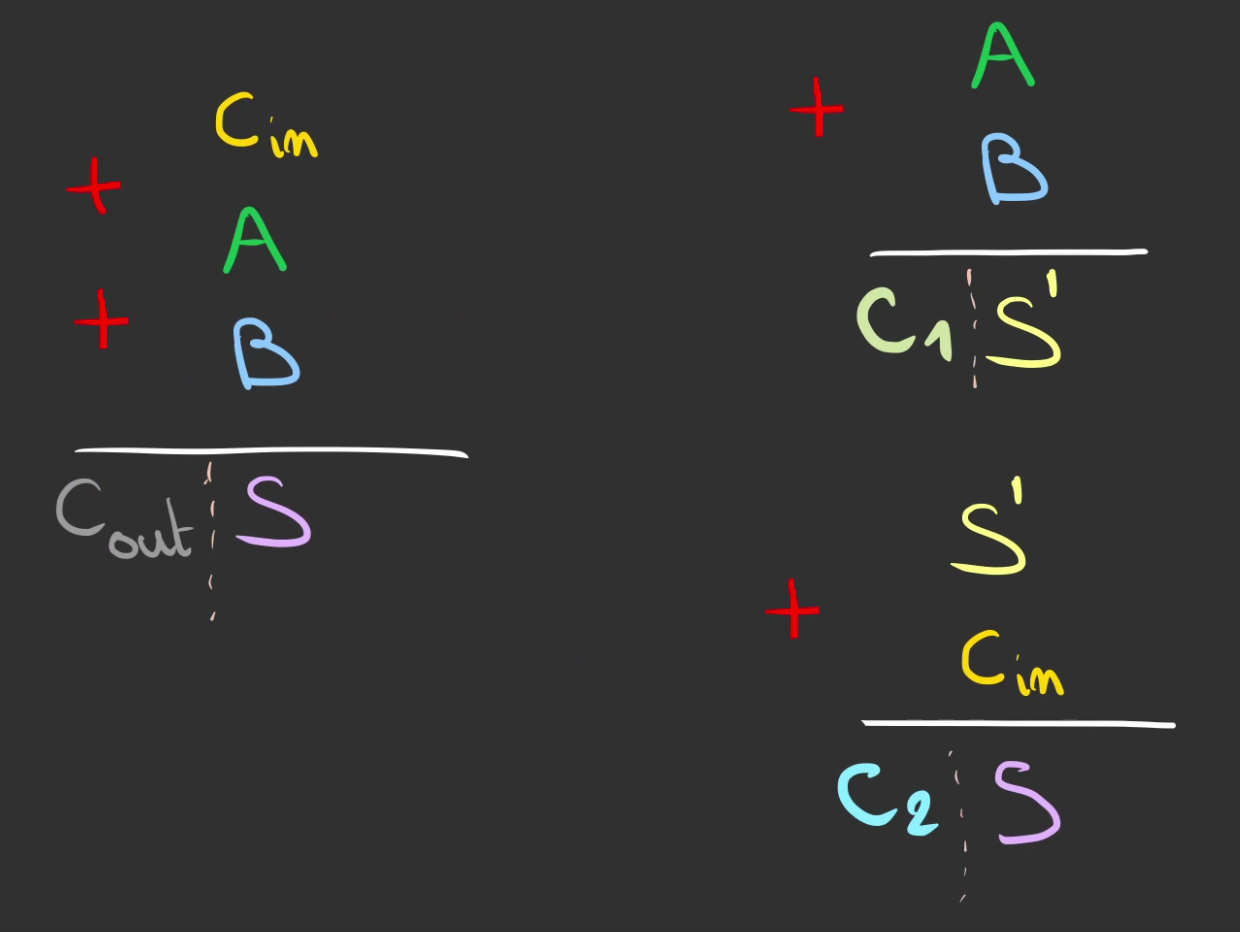
Qu'on peut alors câbler
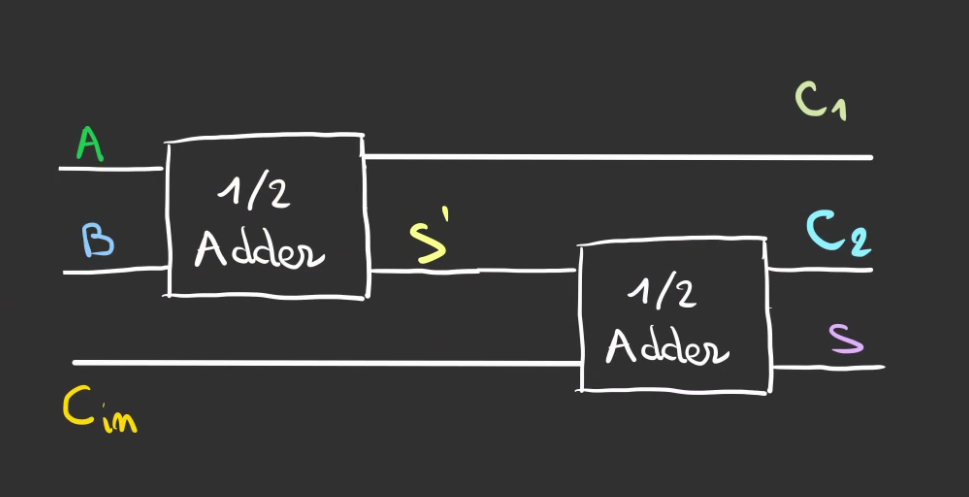
La question est maintenant de savoir comment combiner les retenues.
On sait que $C_{out} = C_1 \space ??? \space C_2$
Plus qu'à déterminer $???$
| $C_{in}$ | A | B | $S'=A \oplus B$ | $C_1 = A \wedge B$ | $C_2 = S' \wedge C_{in} $ | $C_{out}$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
Il en ressort qu'un simple OU suffit, donc:
$$C_{out} = C_1 \vee C_2$$
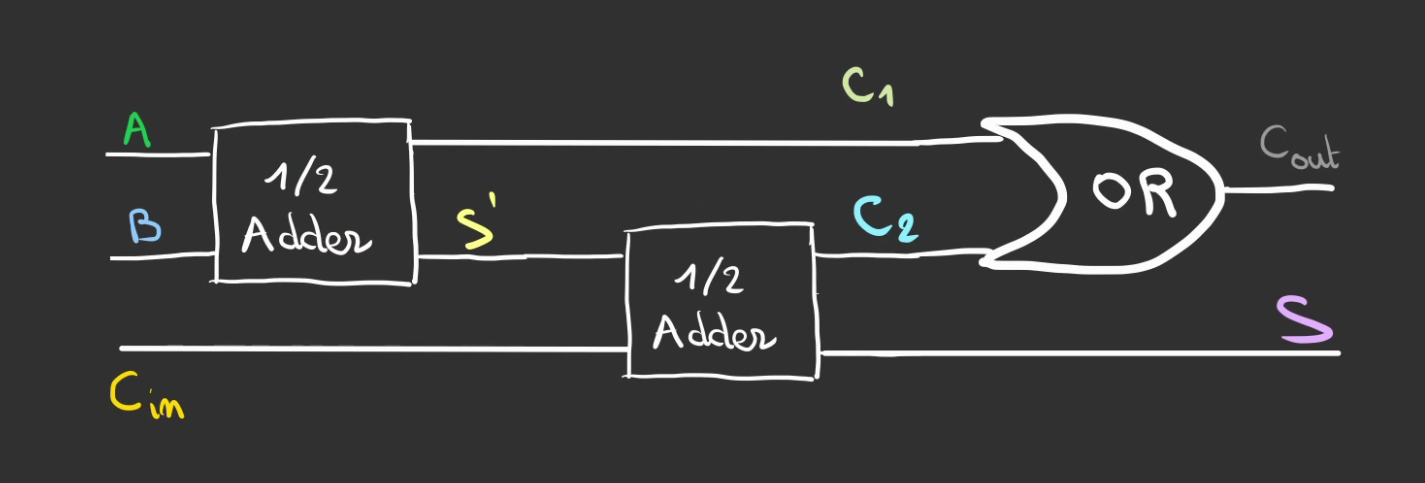
On peut alors faire varier les entrées en fixant la retenue précédente à "1".
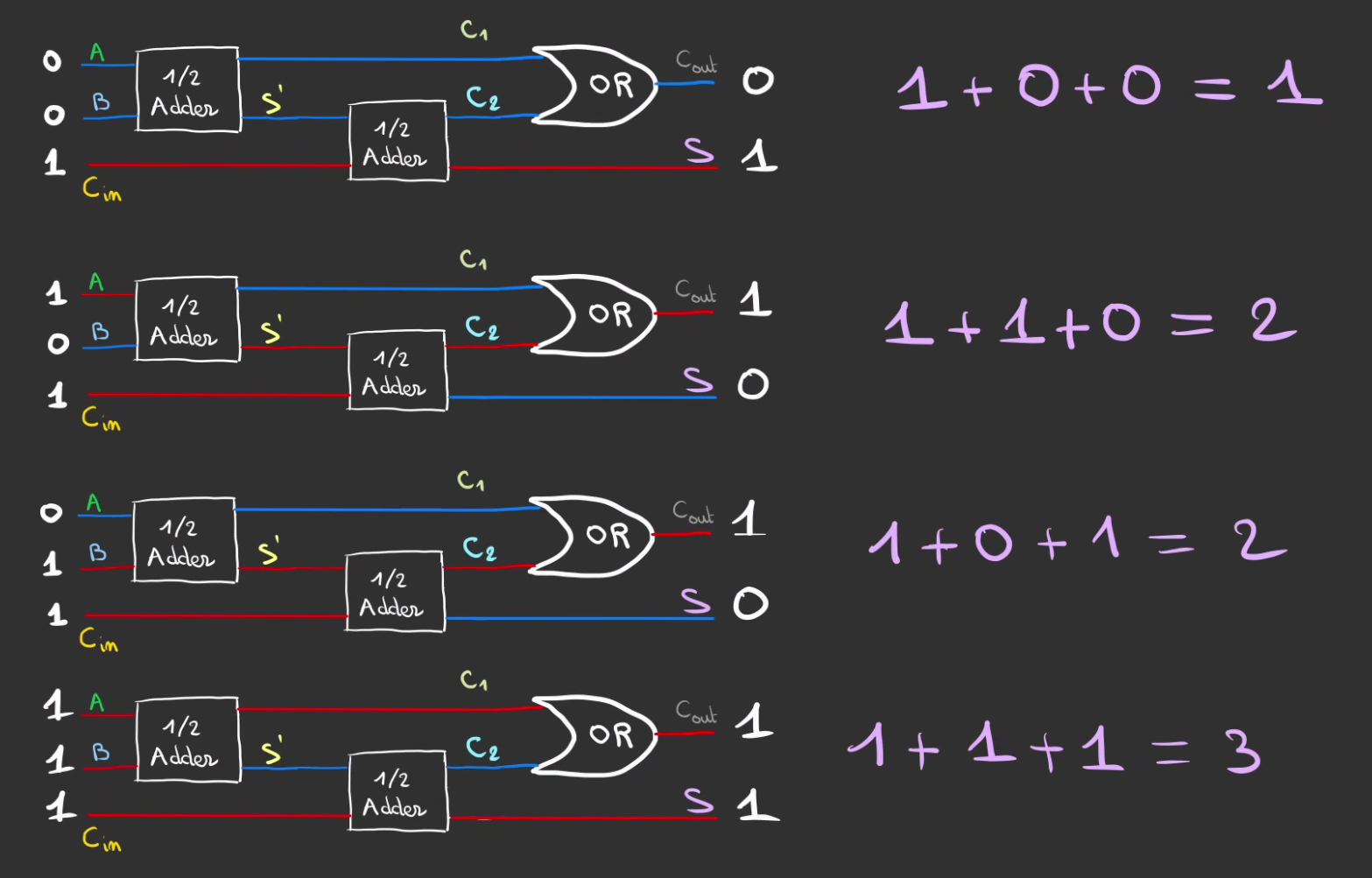
Nickel tout marche ! 🤩
Allez vite on empacte ! 📦
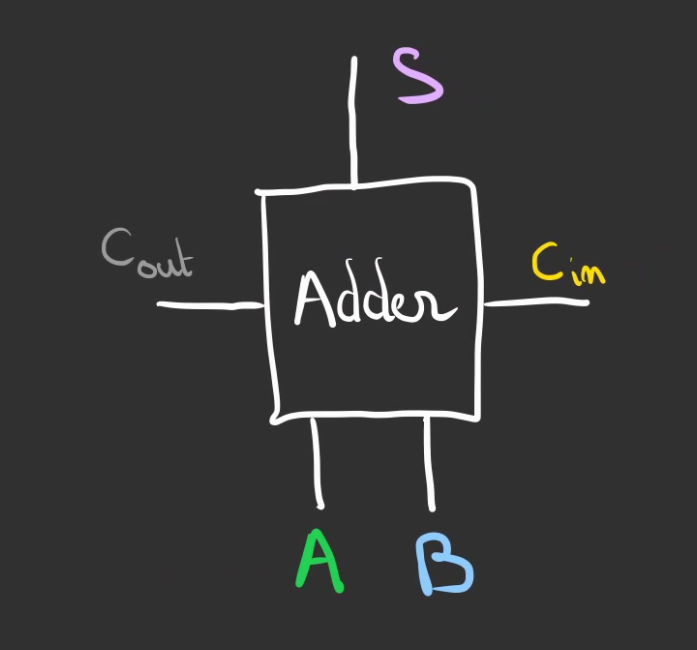
Je mets exprès les retenues sur le côté, ça va nous servir.
RCA
Il est temps de faire notre vraie addition ^^
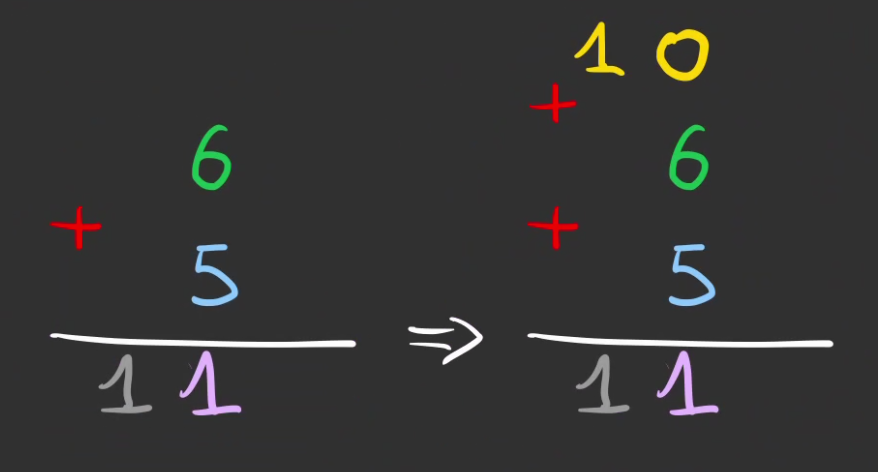
Je mets les retenu en jaune, pour les expliciter.
Pour rappel nous avons cette formulation générale.
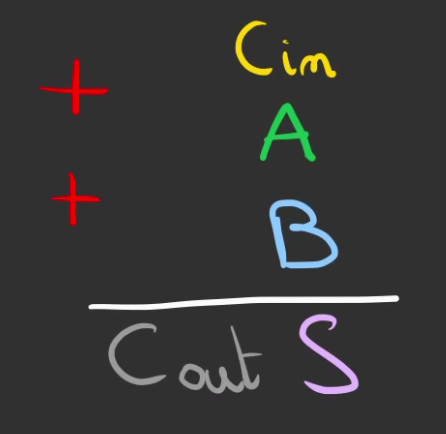
Nous pouvons passer en représentation binaire

Ce qui peut alors se variabiliser en
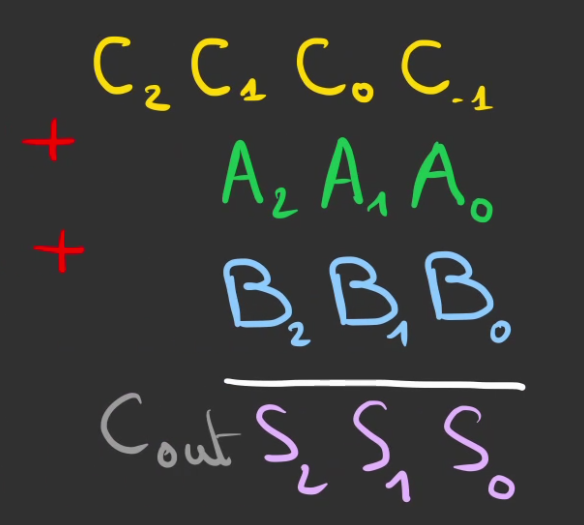
Que l'on cable en
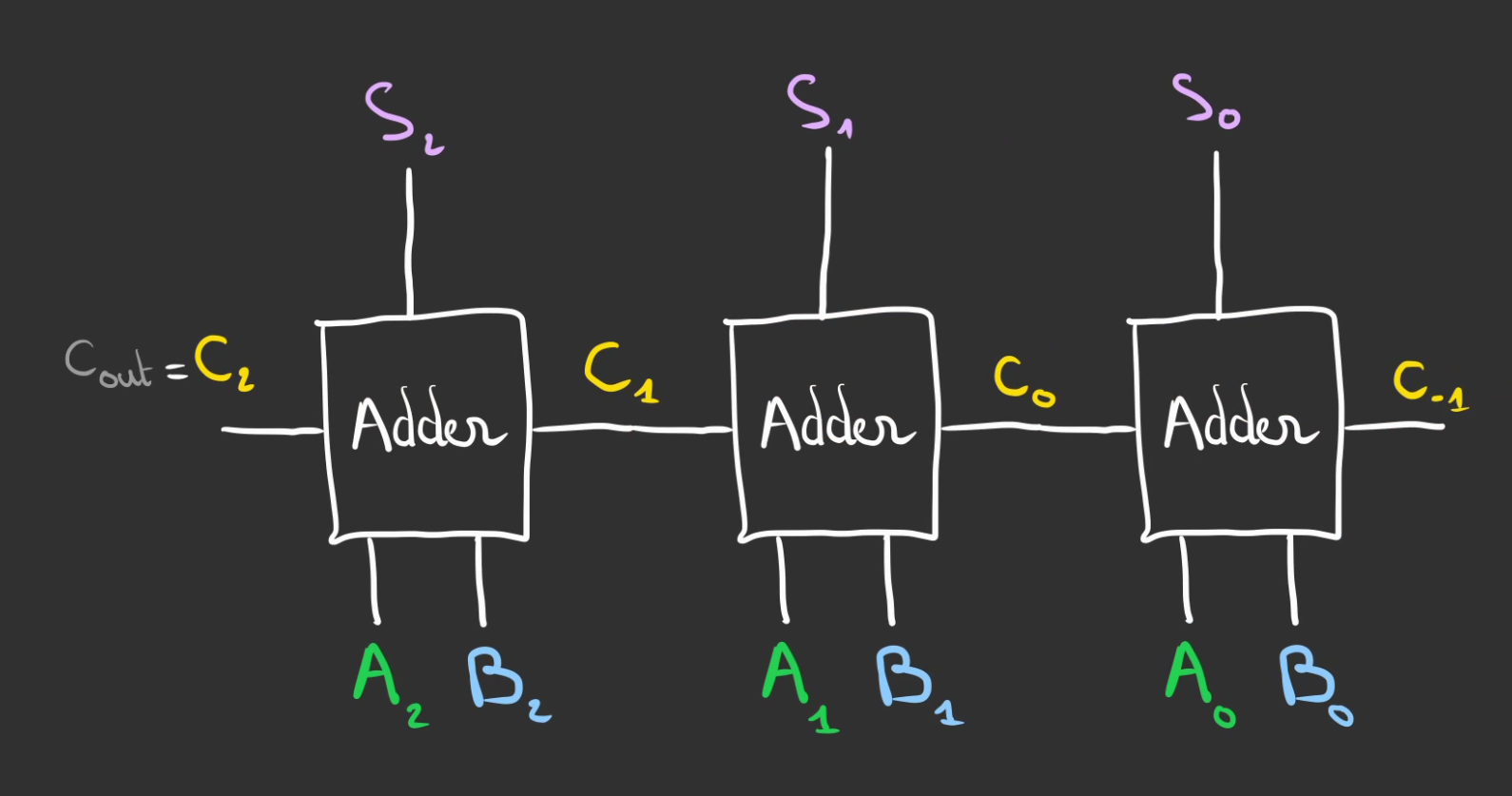
Et oui! On chaîne tout le monde 😁
Chaque bloc est responsable de gérer sa colonne, son bit.
Et propage l'éventuelle retenue au bloc suivant.
En dynamique cela donne.
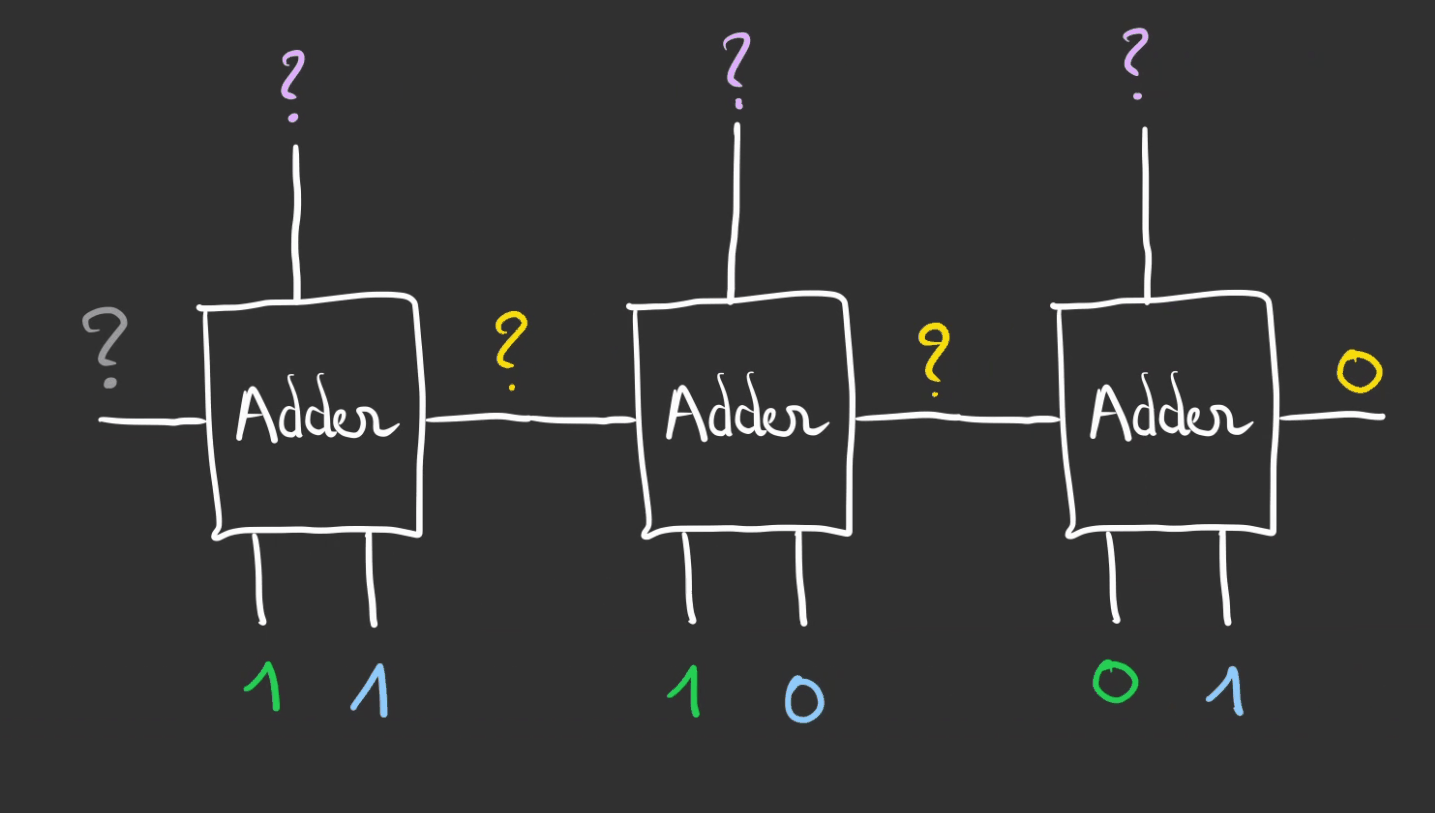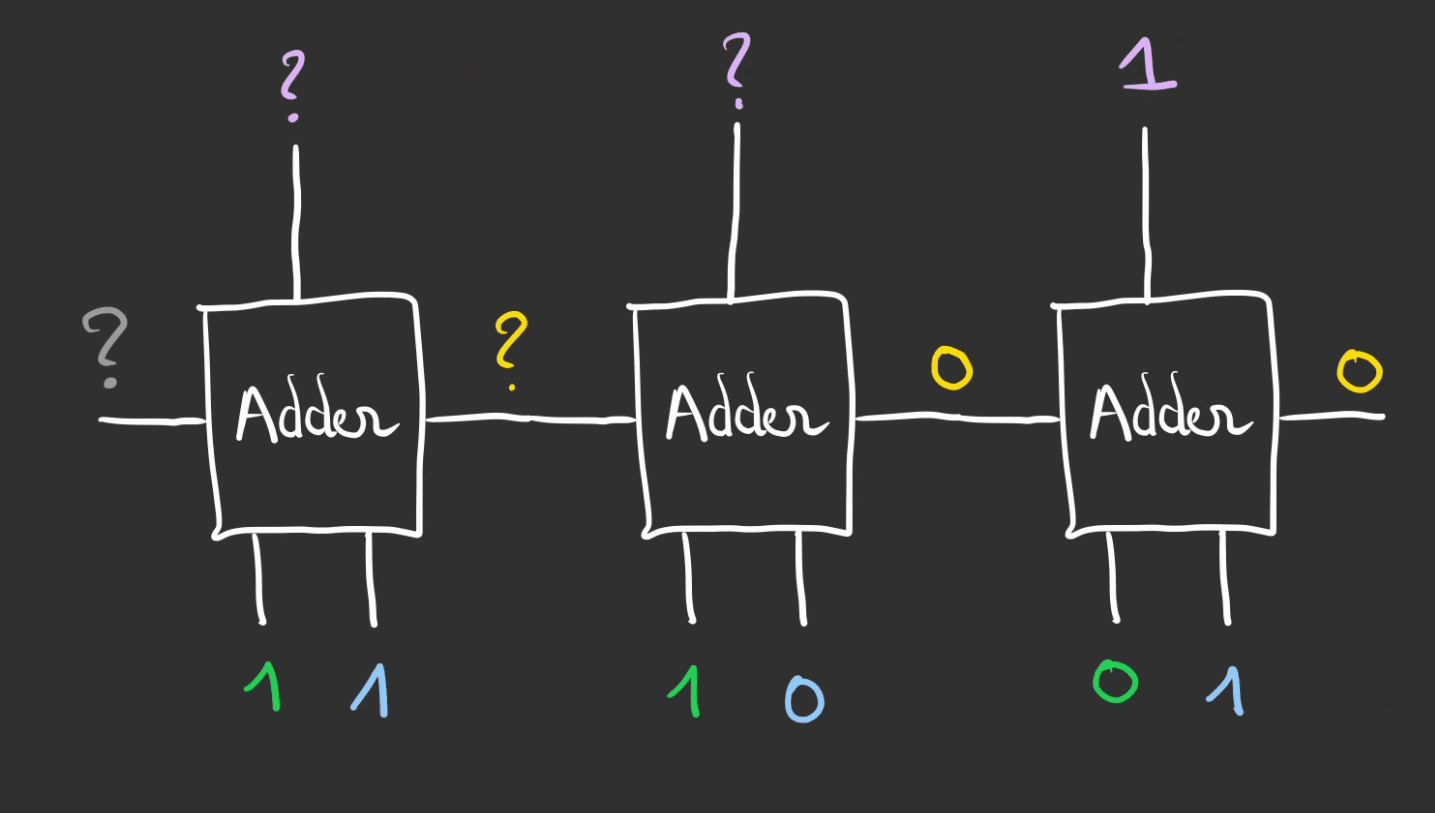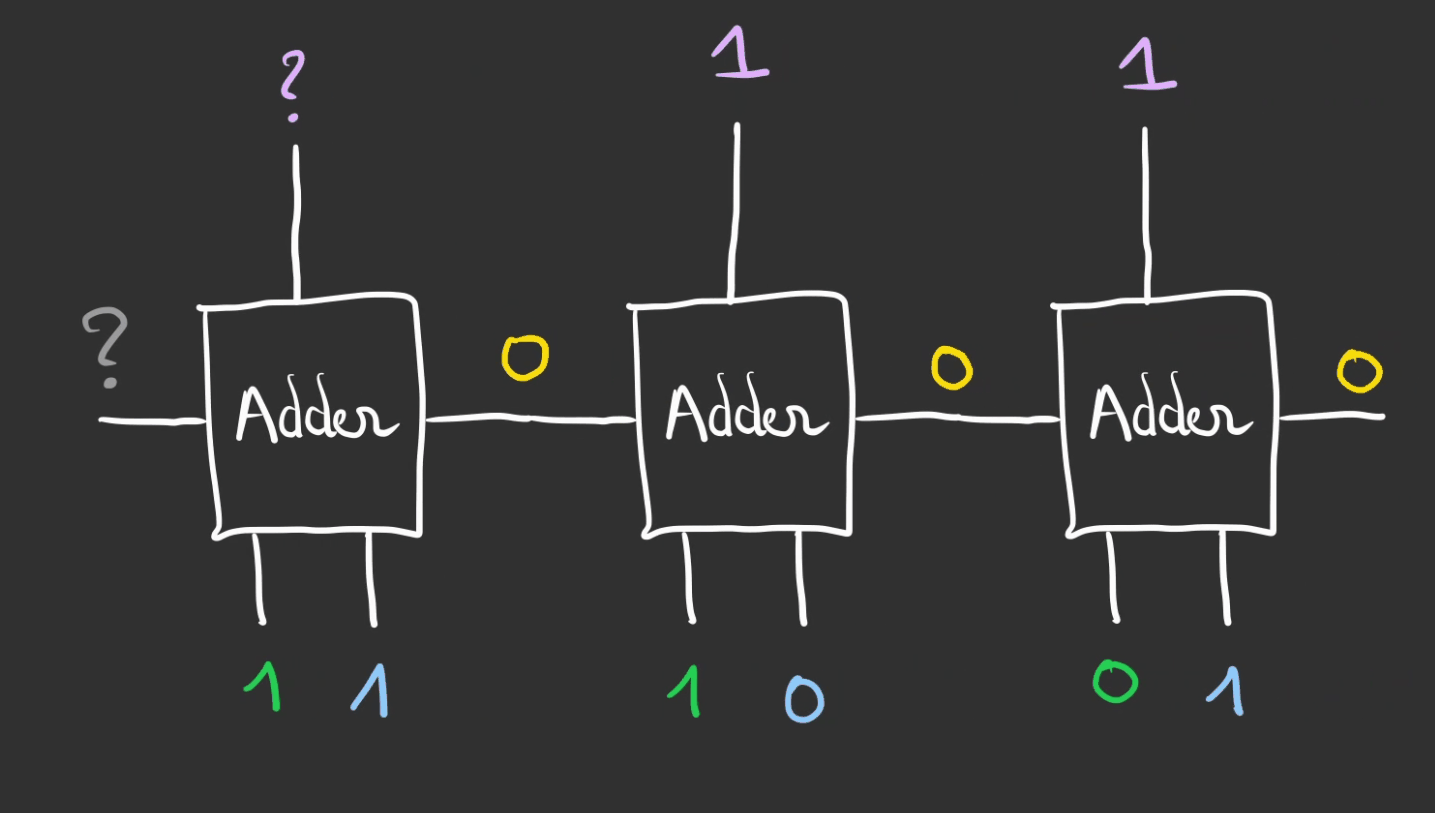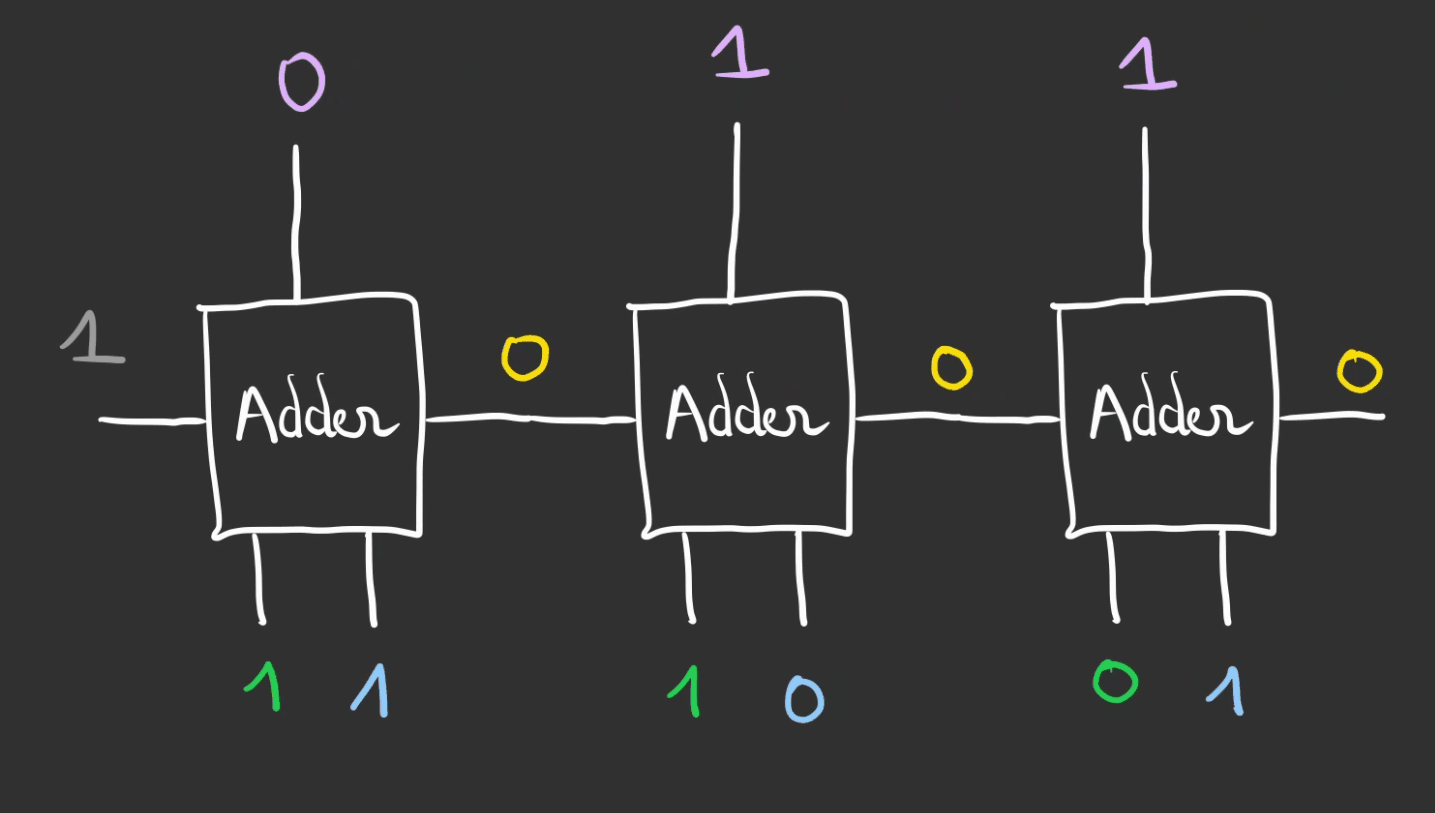
On lit alors le résultat de la gauche vers la droite.
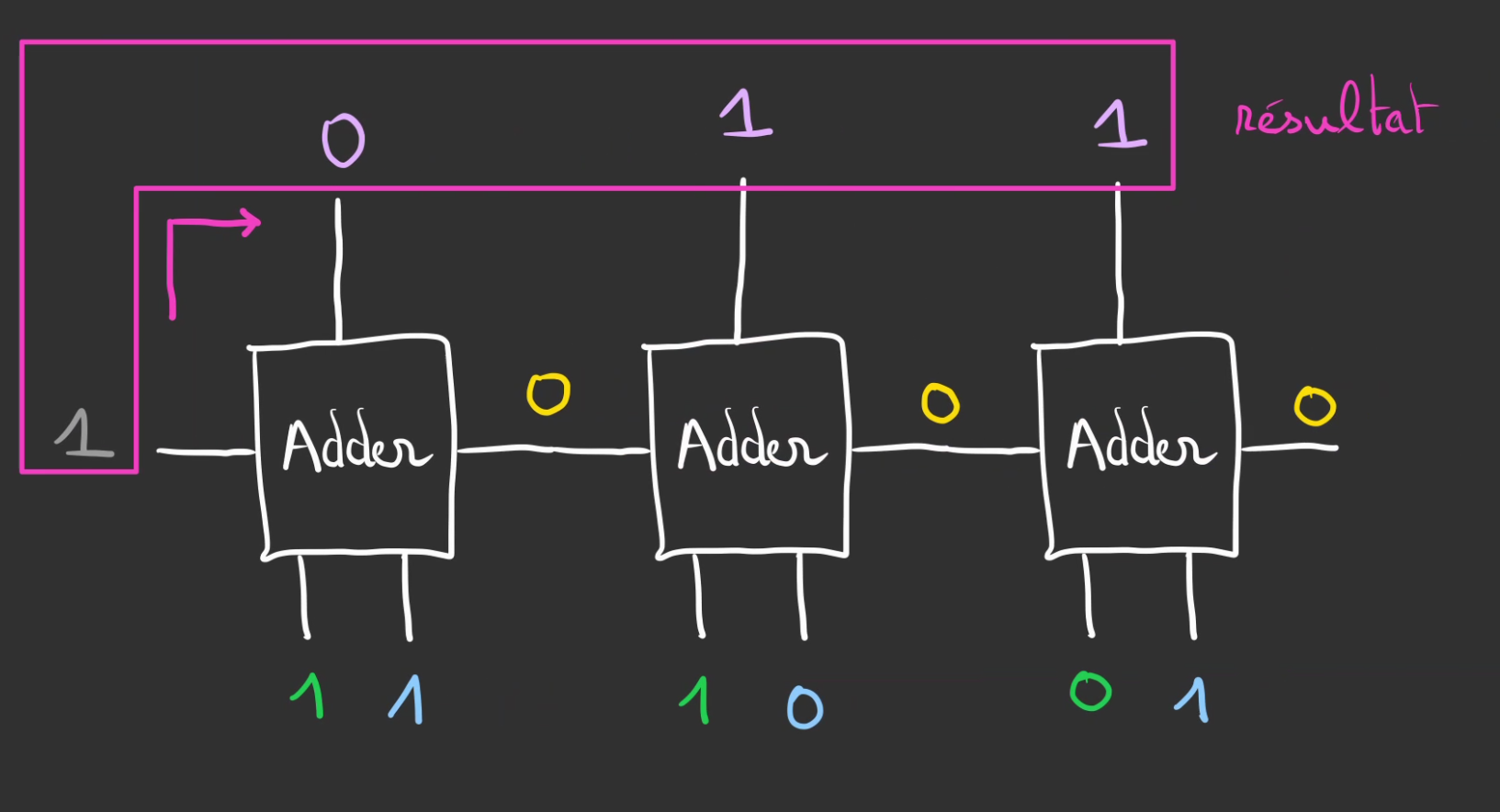
On obtient bien le $6_{10} + 5_{10} => 110_2 + 101_2 = 1011_2 => 11_{10}$
Vous n'êtes pas impressionné parce que la retenue intermédiaire vaut toujours $0$ ?
Ok, essayons $7_{10} + 5_{10} = 12_{10} => 111_2 + 101_2 = ??$
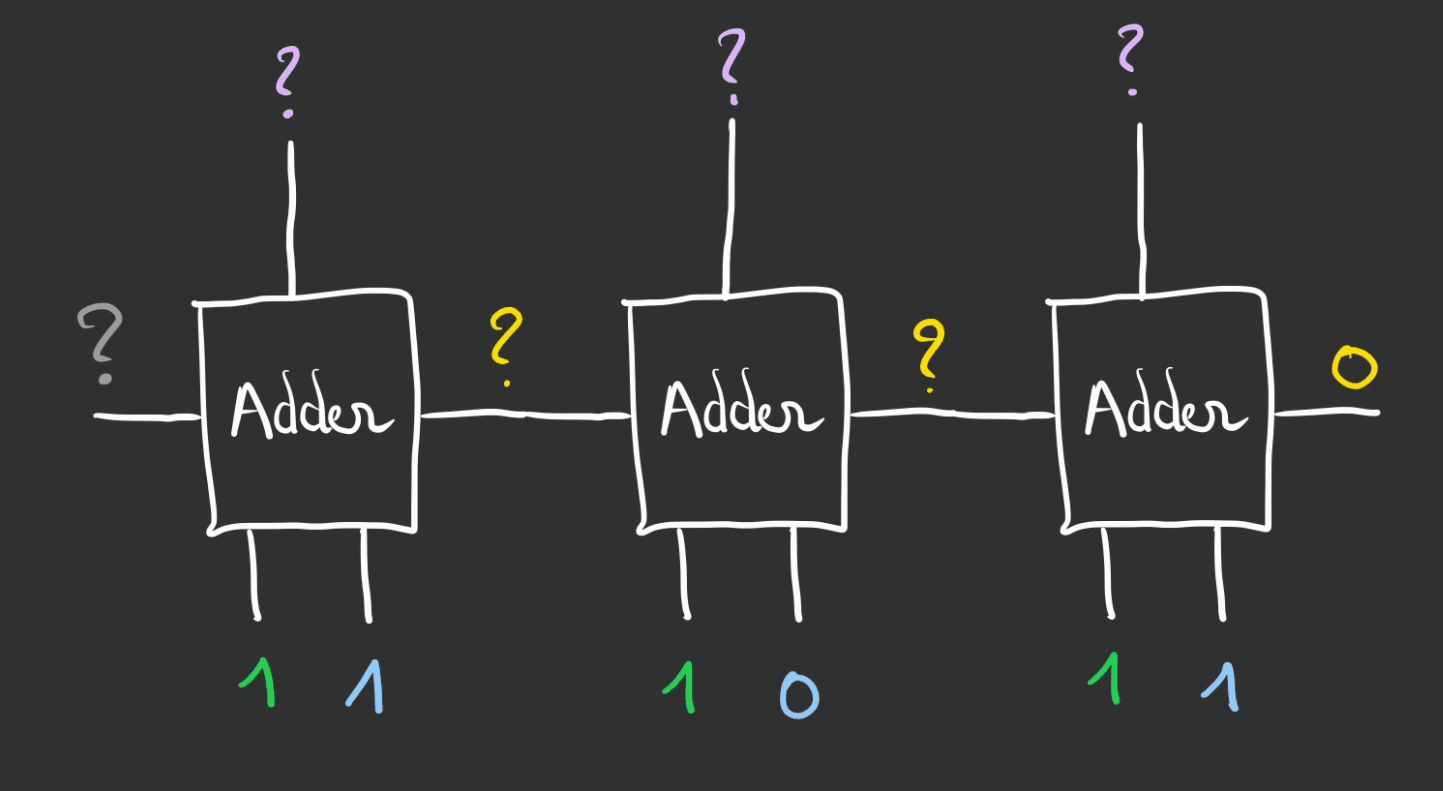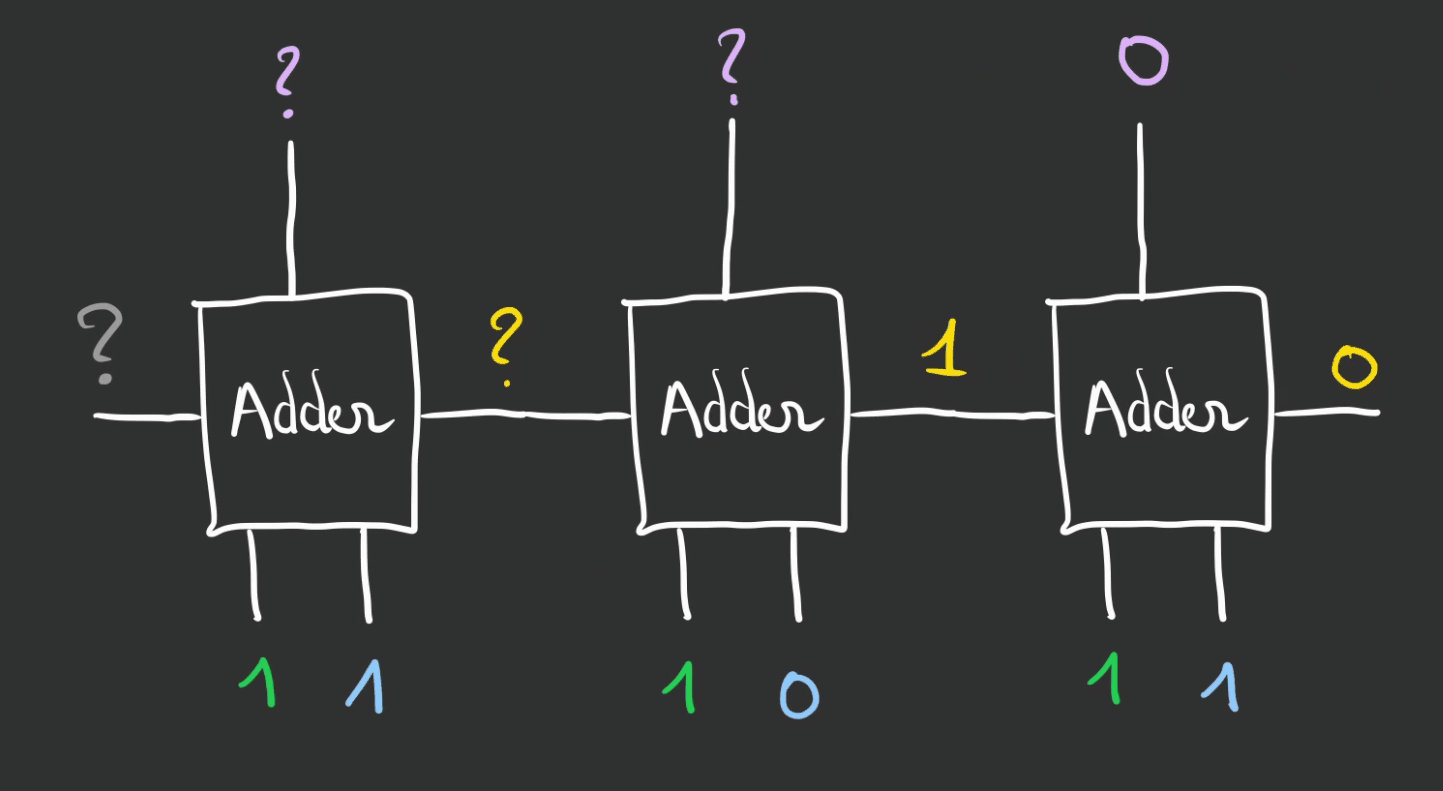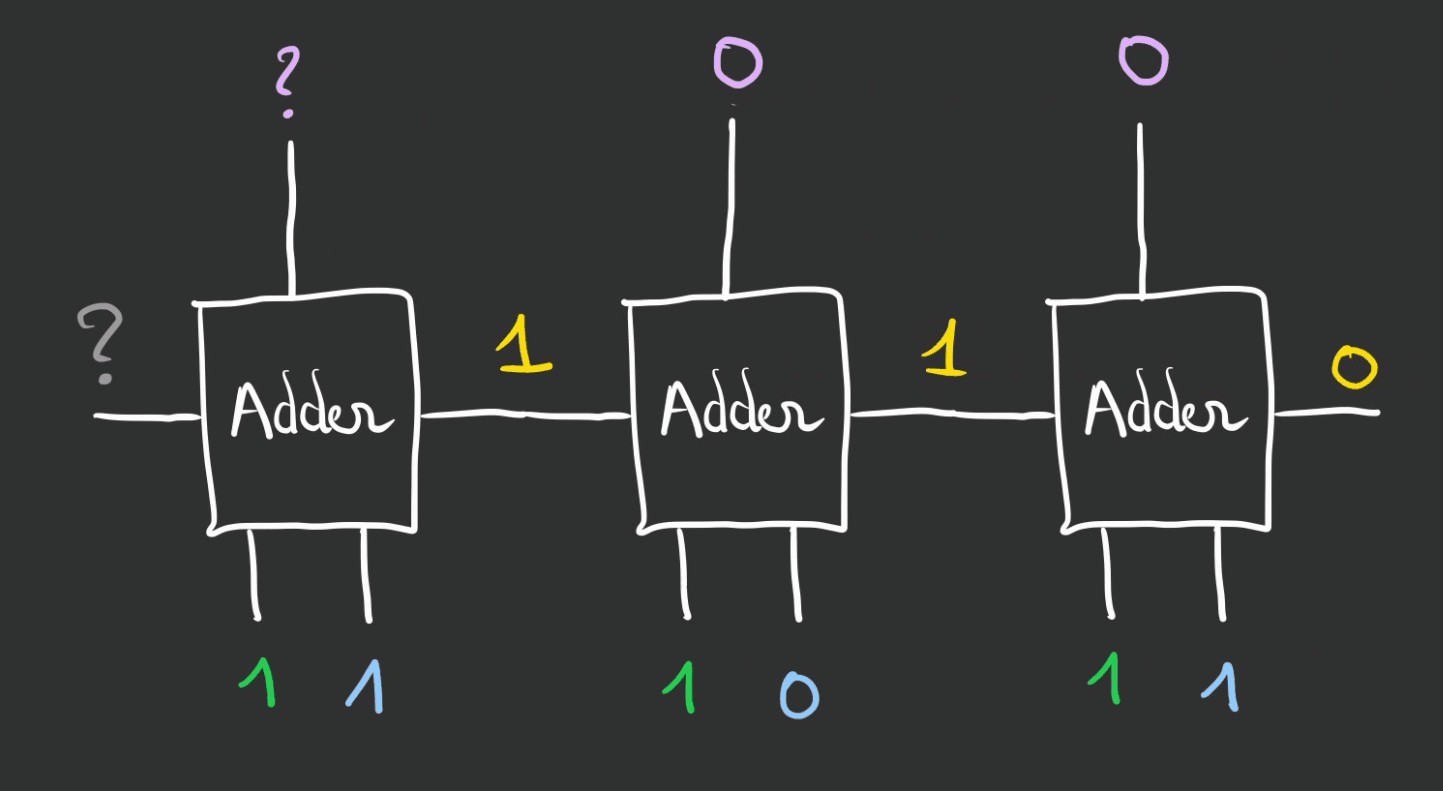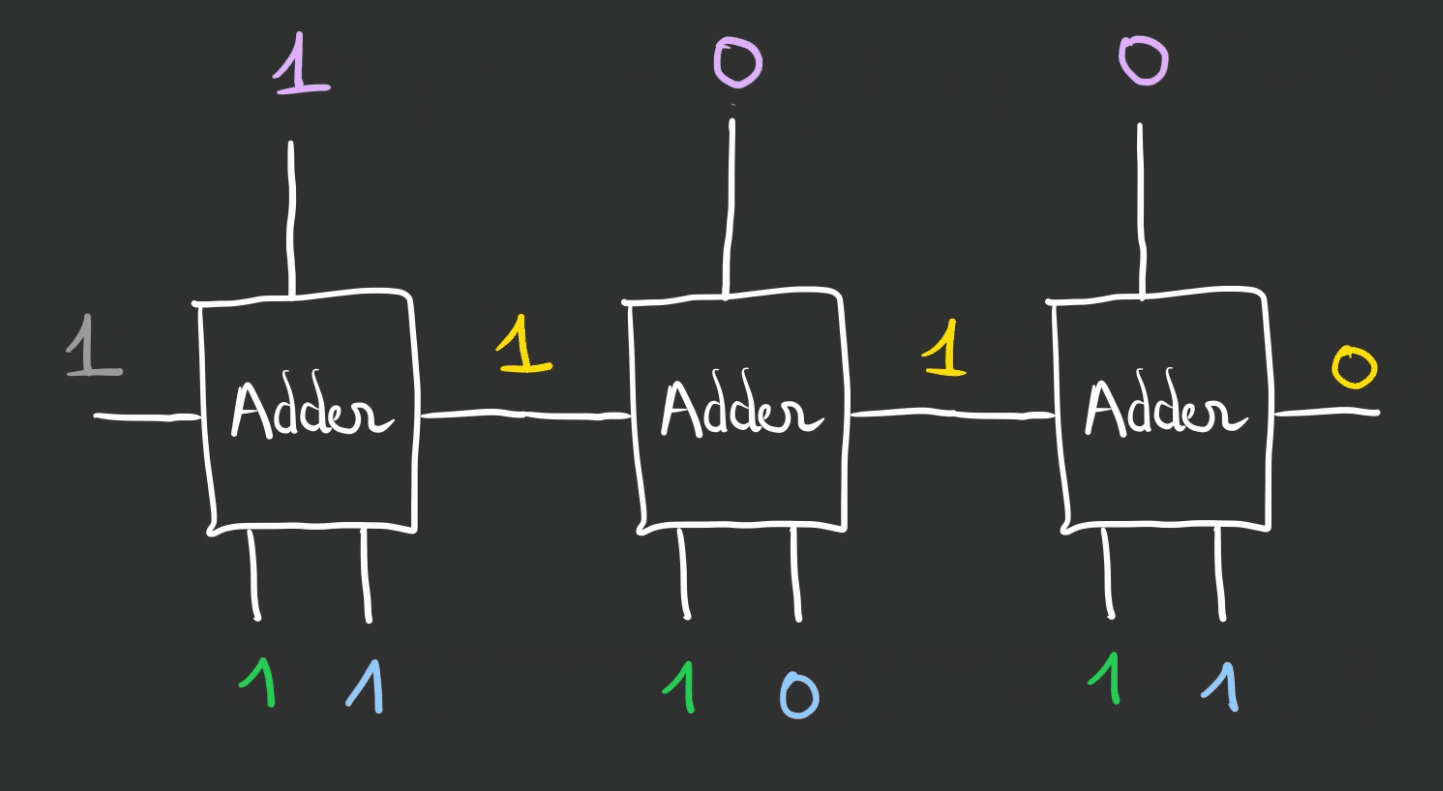
On obtient $1100_2 => 12_{10}$
C'est parfait! On sait additionner deux nombres !
On peut alors généraliser à n bits.
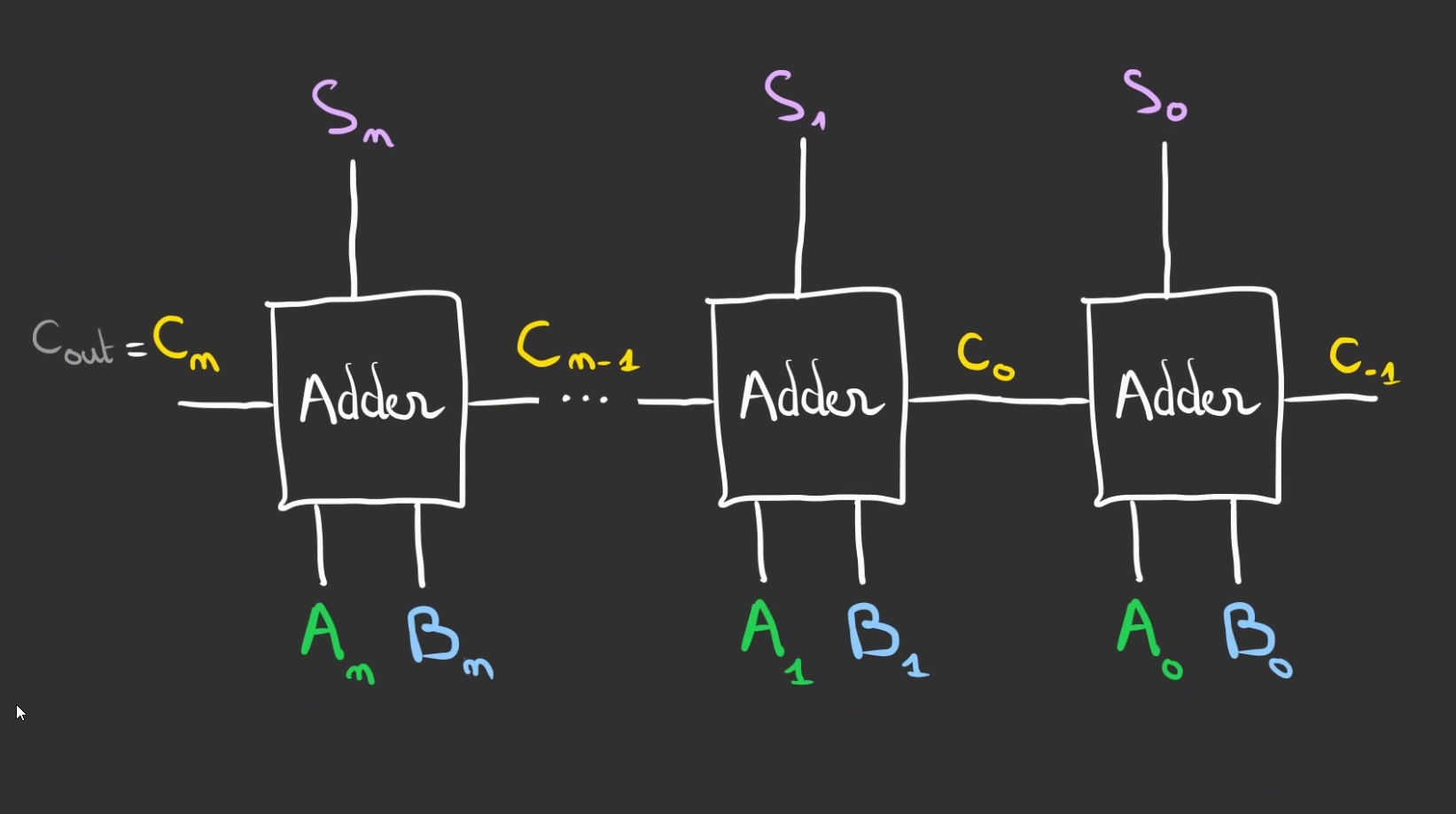
Le fait de répercuter la retenu d'un étage à l'autre, donne son nom à ce montage, que nomme Riple Carry Adder.
Ripple car cela fait penser aux ricochets à la surface de l'eau. ^^
On peut alors en faire une boîte générale
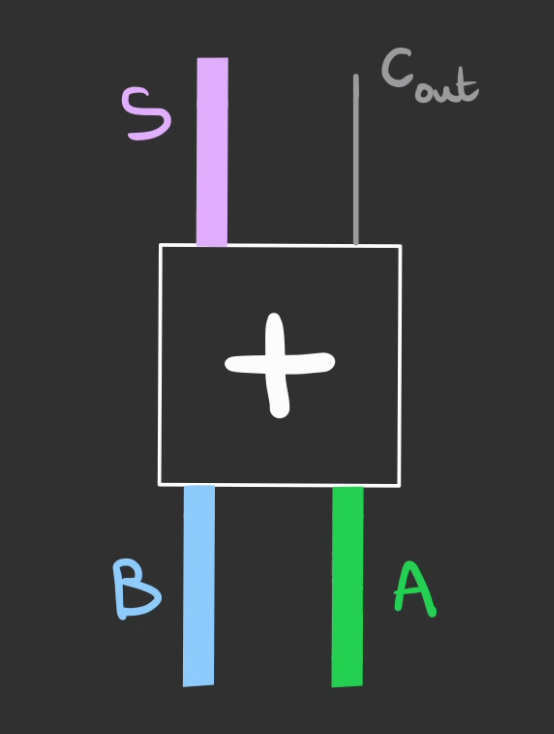
Elle additionne deux bus de données $A$ et $B$. Et produit un bus $S$ et un signal $C_{out}$ qui si il est a $1$ signifie que le nombre additonné est trop grand pour le bus de sortie.
La largeur du bus conditionne jusqu'à combien le résultat de l'addition est valide.
CLA
Mais ces ricochets posent un soucis.
Cela prends du temps de propager la retenue d'un étage à l'autre.
Oui parce que je n'en n'est pas trop parlé.
Mais chaque transistor qui compose les portes qui composent les additionneurs prends un certains temps à commuter.
Ce qui veut dire que la retenu, mets un certain temps à arriver qui correspond à la combinaisons (certains en parrallèle d'autre en série) des temps de commutation des transistors.
Donc si on note $T_{a}$ le temps pour obtenir le résultat d'un additionneur.
Alors la durée pour obtenir le résultat final est la somme des $T_{a}$
Du coup $T = n * T_a$ où $n$ est le nombres de bits et donc le nombre d'additionneur.
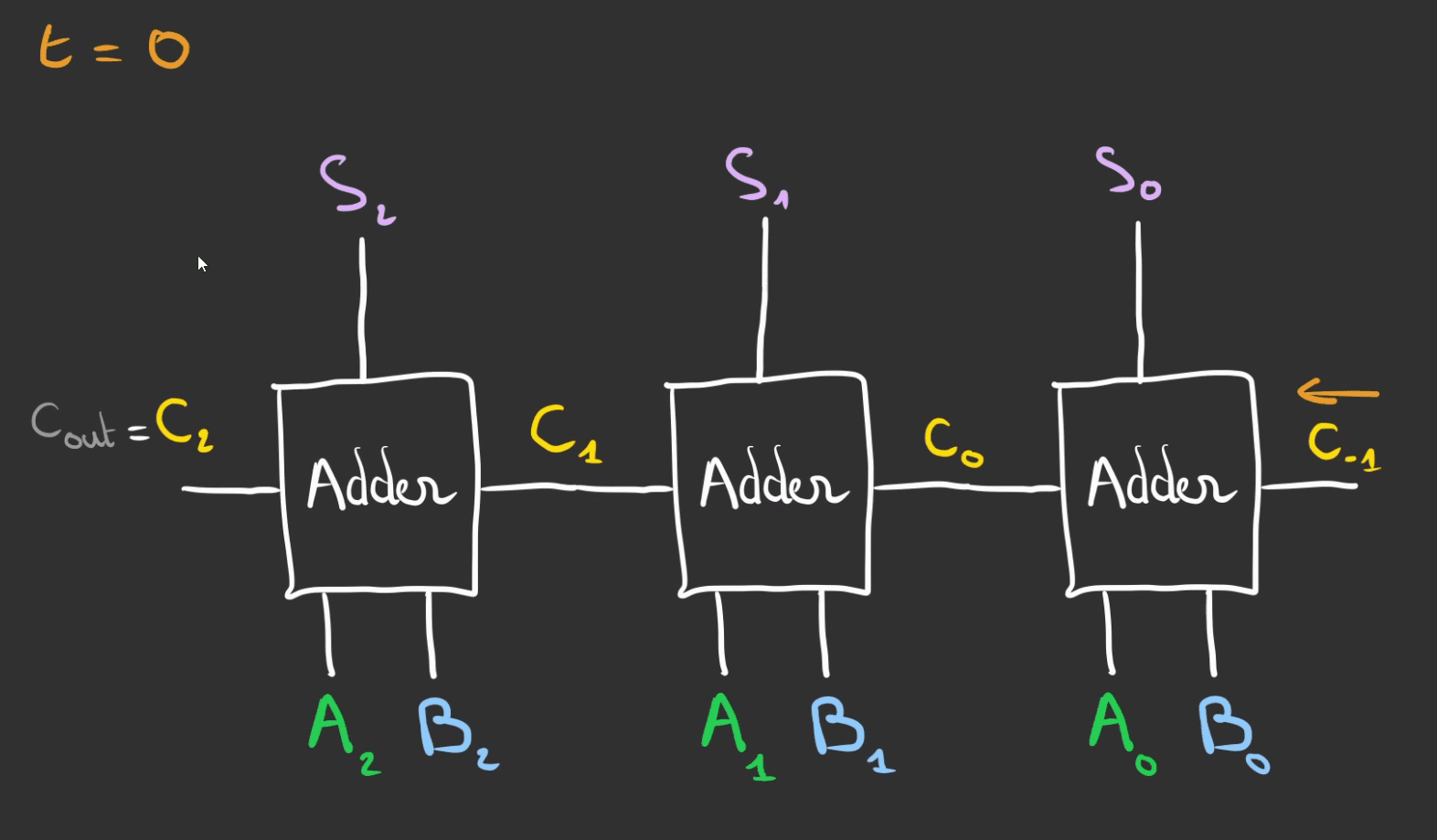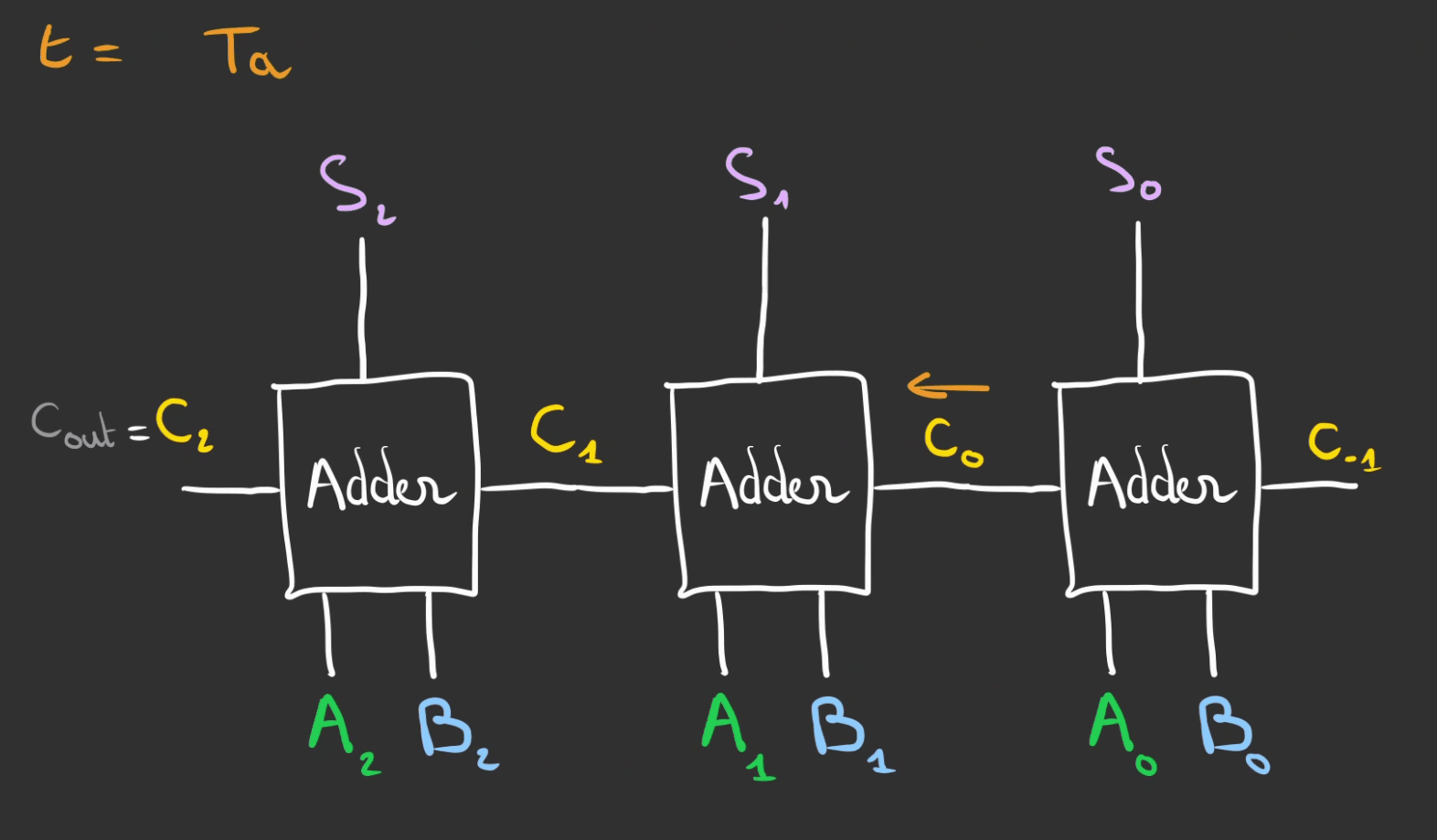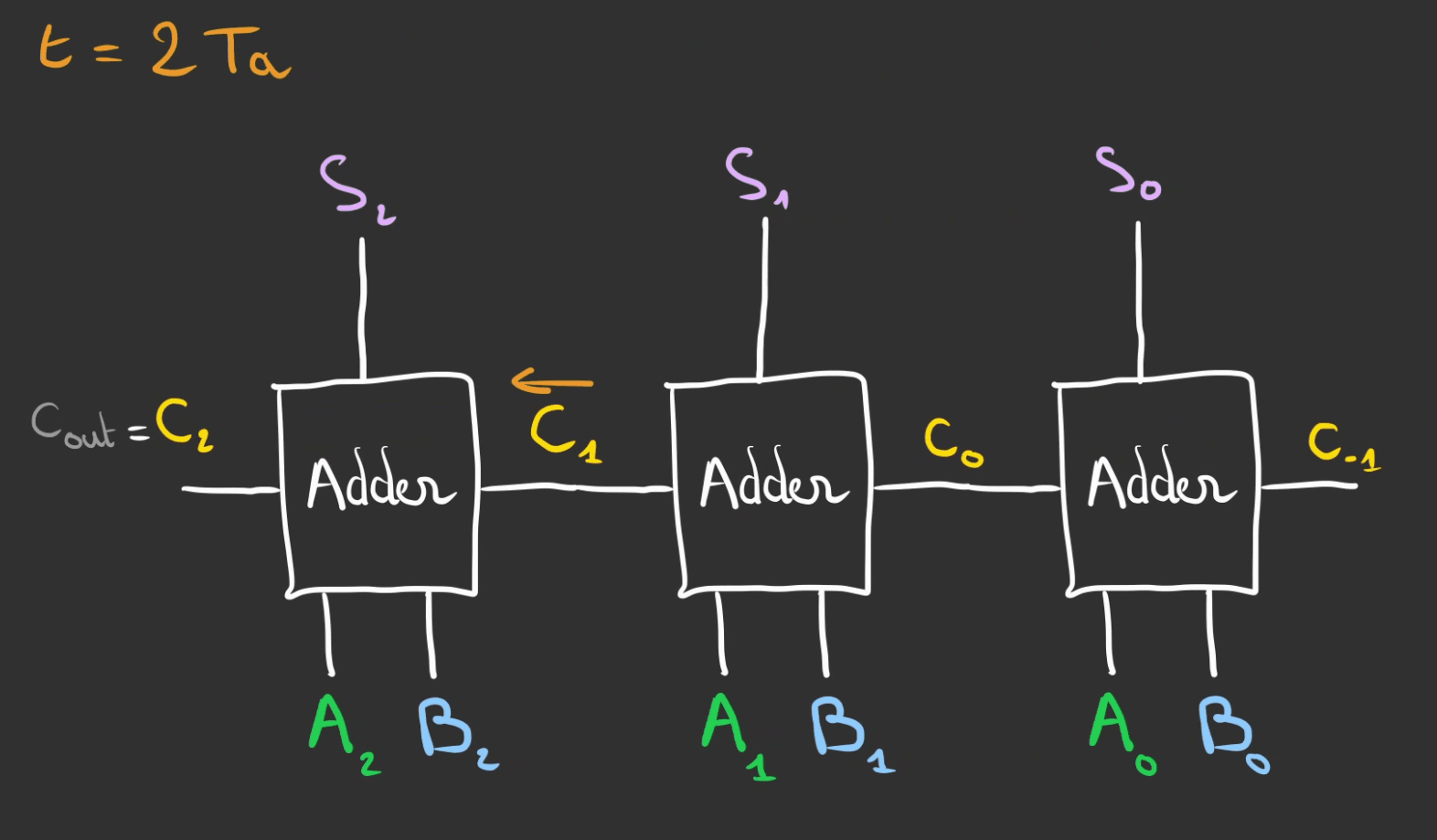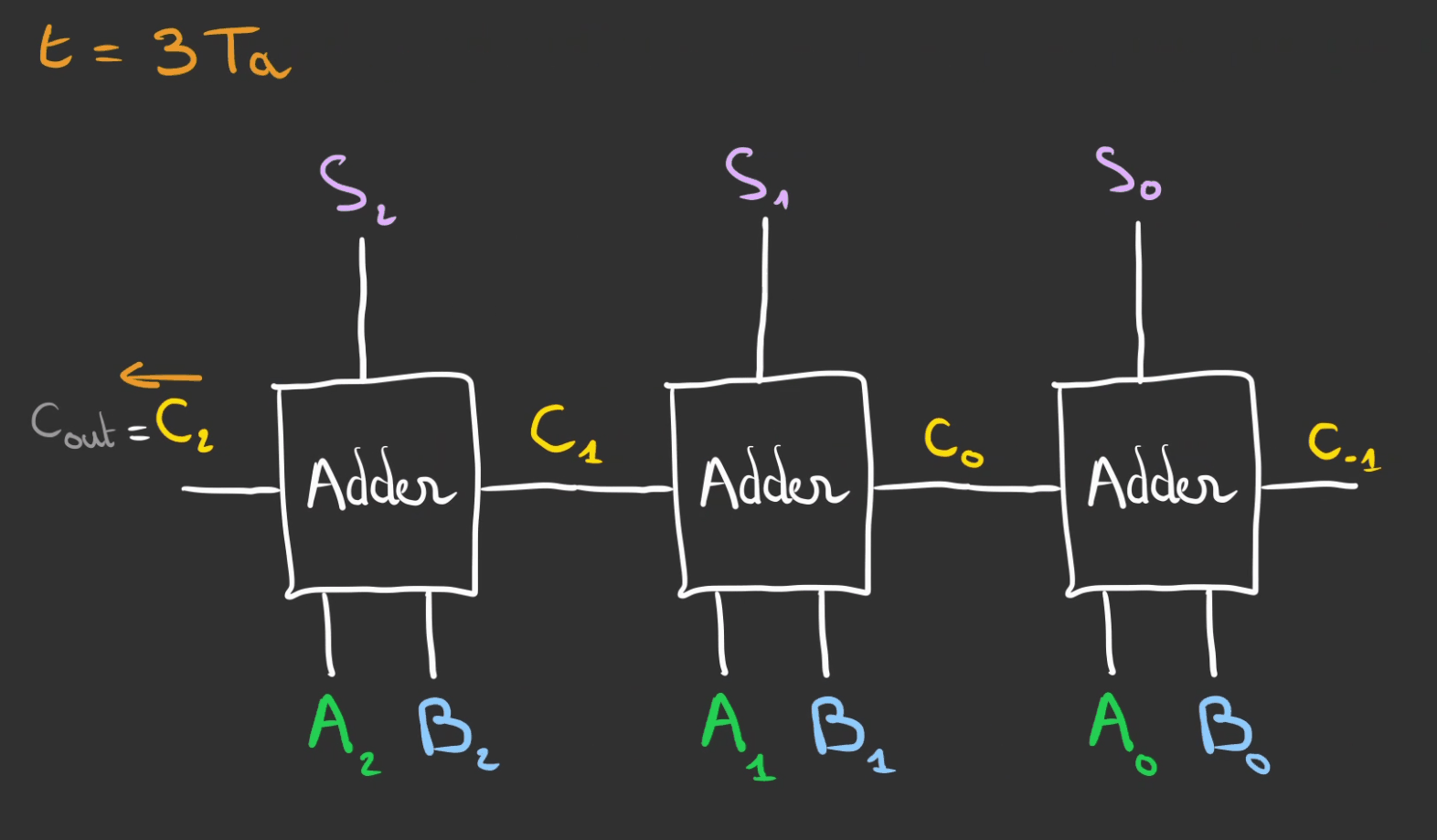
On va devoir être plus malin et réfléchir différemment.
Qu'est ce qui est parrallélisable et qu'est ce qui ne l'est pas.
| $C_{in}$ | A | B | $C_{out}$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
On sort
$$ C_{out} = (\overline{C_{in}} \wedge A \wedge B) \vee (C_{in} \wedge A \wedge \overline{B}) \vee (C_{in} \wedge \overline{A} \wedge B) \vee (C_{in} \wedge A \wedge B) $$ On peut factoriser $$ C_{out} = [(A \wedge B) \wedge (C_{in} \vee \overline{C_{in}})] \vee [C_{in} \wedge ((A \wedge \overline{B}) \vee (\overline{A} \wedge B))] $$ Or $$ (A \wedge \overline{B}) \vee (\overline{A} \wedge B) = A \oplus B $$ Et $$C_{in} \vee \overline{C_{in}} = 1$$ donc $$(A \wedge B) \wedge (C_{in} \vee \overline{C_{in}}) = A \wedge B) \wedge 1$$ Or $$X \wedge 1 = X$$ Donc $$ (A \wedge B) \wedge (C_{in} \vee \overline{C_{in}}) = A \wedge B $$Algèbre de Boole
Finalement
$$ C_{out} = C_{in} \wedge ( A \oplus B ) \vee (A \wedge B) $$
On pose alors
$$\begin{cases} P = A \oplus B\space(propagateur)\\
G = A \wedge B \space (générateur) \end{cases} $$
Si $P$ est vrai la retenu se propage, si $G$ est vrai, la retenue se génère, d'où les noms.
On observe que ces deux valeurs sont complètement disjointes des retenues et donc parallélisable.
Le gros du travail est alors de déterminer les retenues
Ainsi
$$ C_{out} = (C_{in} \wedge P) \vee G $$
On généralise
$$ \begin{cases} C_{n} = (C_{n-1} \wedge P_n) \vee G_n \\ Ce qui donne $$\begin{cases} C_{0} = (C_{-1} \wedge P_0) \vee G_0 \\ Or $C_{-1} = 0$ car il n'y a pas de retenu au début Donc $C_{0} = P_0 \vee G_0$ On remplace $$\begin{cases} C_{0} = P_0 \vee G_0 \\ On développe $$\begin{cases} C_{0} = P_0 \vee G_0 \\ On remplace $$\begin{cases} C_{0} = P_0 \vee G_0 \\
P_n = A_n \oplus B_n \\
G_n = A_n \wedge B_n \end{cases} $$Algèbre de Boole
C_{1} = (C_{0} \wedge P_1) \vee G_1 \\
C_{2} = (C_{1} \wedge P_2) \vee G_2 \\
\end{cases} $$
C_{1} = ([P_0 \vee G_0] \wedge P_1) \vee G_1 \\
C_{2} = (C_{1} \wedge P_2) \vee G_2 \\
\end{cases} $$
C_{1} = ([P_1 \wedge P_0] \vee [P_1 \wedge G_0]) \vee G_1 \\
C_{2} = (C_{1} \wedge P_2) \vee G_2 \\
\end{cases} $$
C_{1} = [P_1 \wedge P_0] \vee [P_1 \wedge G_0] \vee G_1 \\
C_{2} = [[P_1 \wedge P_0] \vee [P_1 \wedge G_0] \vee G_1] \wedge P_2) \vee G_2 \\
\end{cases} $$
Finalement
$$\begin{cases} C_{0} = P_0 \vee G_0 \\
C_{1} = [P_1 \wedge P_0] \vee [P_1 \wedge G_0] \vee G_1 \\
C_{2} = [P_2 \wedge P_1 \wedge P_0] \vee [ P_2 \wedge P_1 \wedge G_0] \vee [P_2 \wedge G_1] \vee G_2 = C_{out} \\
\end{cases} $$
Cela donne grosso modo ça
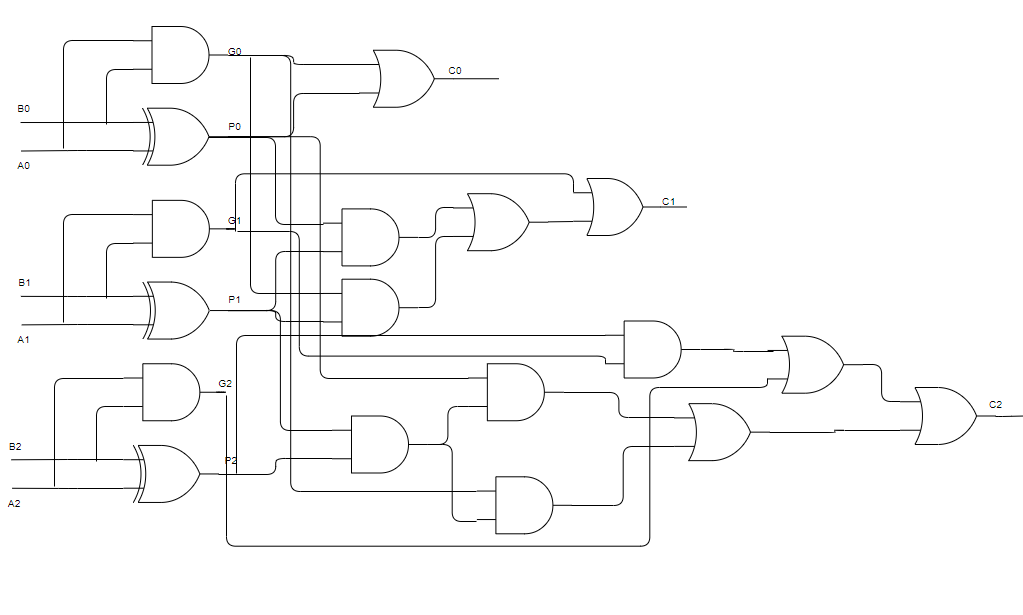
C'est le bazar, hein ? 🤣
On va mettre tout ça dans une boîte et ne plus y penser 😁
l'important c'est que l'on a les retenues de tous les étages sans propagation.
Donc il suffit de brancher nos additionneur de 1 bits à la boîte magique.
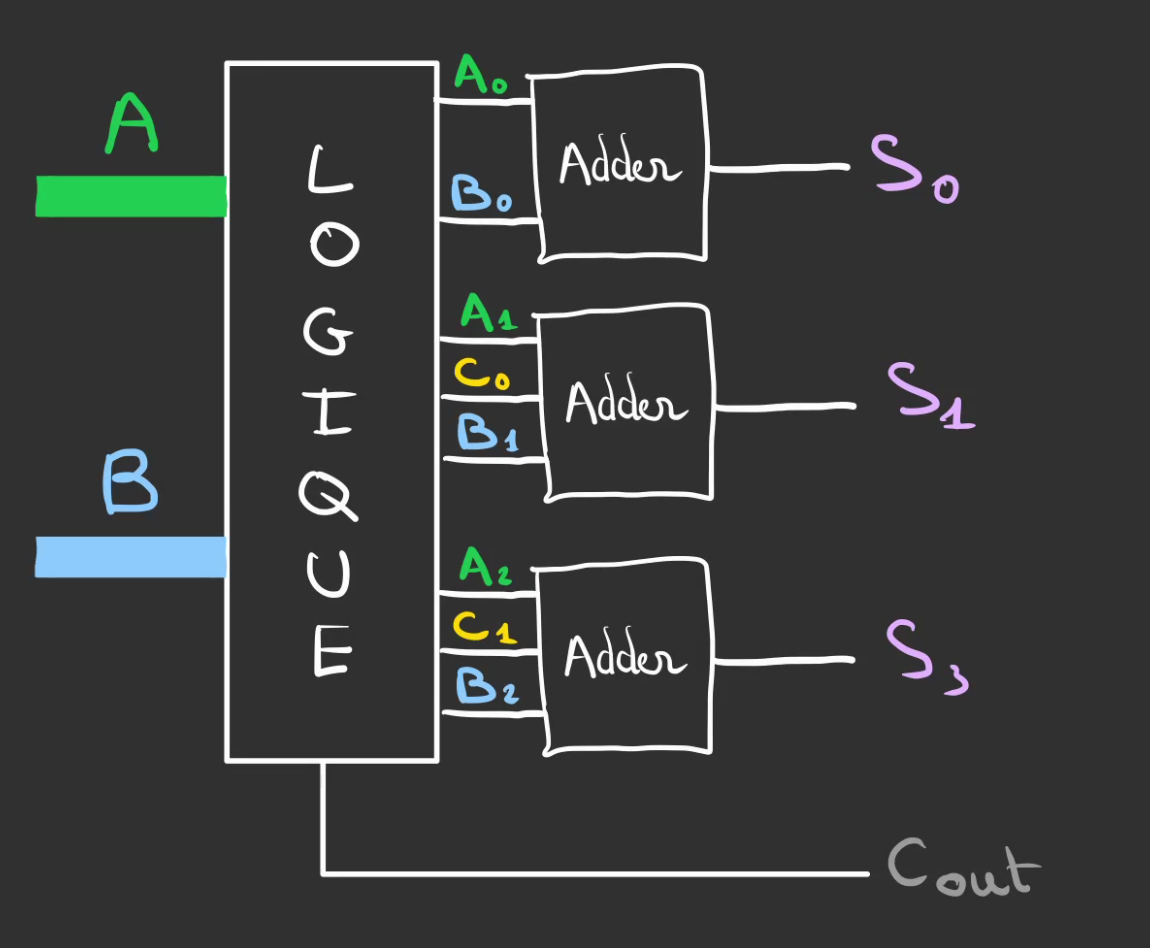
On a donc un système qui est capable de nous donner $S$ sans avoir à attendre les différents étages vu que tout se fait en parrallèle.
Merci la black magic de la boîte. 😄
Vous venez de créer un Carry Look Ahead, prévision de retenue.
Mais attention, plus la boîte est compliqué plus le temps de générations des retenues devient grand, et peut si on a beaucoup de bits et donc de retenues à calculer dépasser le temps de propagation du RCA.
En effet les équation deviennent de plus en plus compliqué je vous laisse faire $C_{32}$ 😏
Conclusion
Oui additionner des nombres c'est pas de la tarte ^^
Merci de votre lecture ❤️
Ce travail est sous licence CC BY-NC-SA 4.0.