Les bases de nombres
Base 10
Lorsque vous demandez à un petit enfant de compter, il va généralement le faire sur ses doigts: 1, 2, 3, ..., 9, 10.
C'est alors qu'il va y avoir un retour à 1 avec un "je sais pas compter après 10 🥺".
On peut donc représenter cela sous la forme d'une roue graduée.
On introduit le 0 et on enlève le 10.
On lit la valeur sur la graduation rouge.
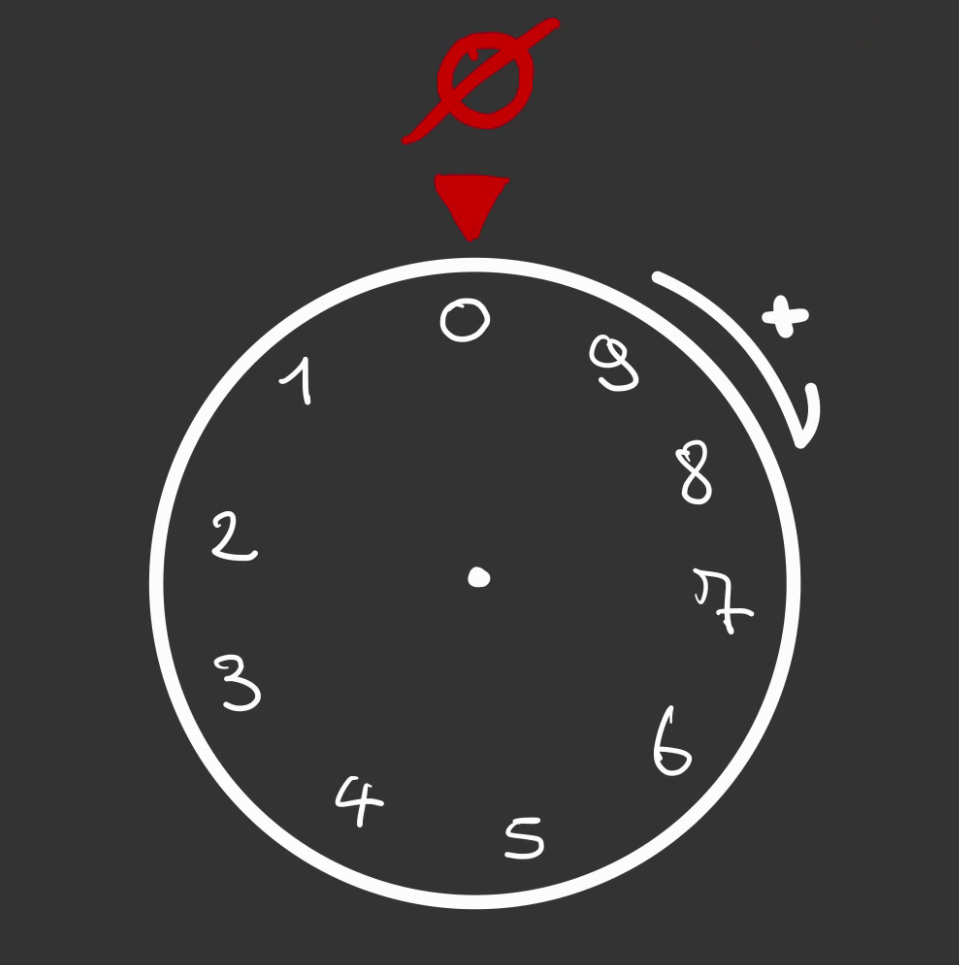
Chaque fois que l'on tourne la roue, on avance d'une graduation.

Et l'on peut aller comme cela, jusqu'à la graduation 9.
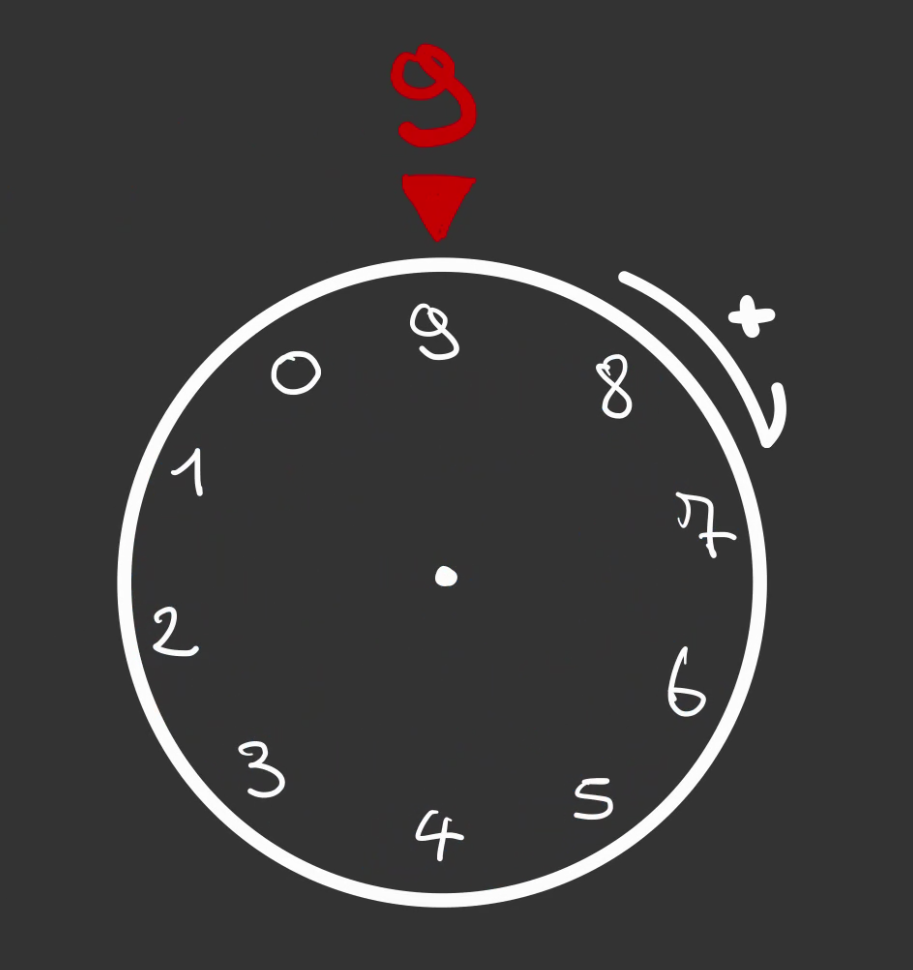
Si on tourne la roue une fois de plus, on revient à 0.

On ne peut donc pas compter jusqu'à 10 sur cette roue.
Sauf si on est ingénieux. 😎
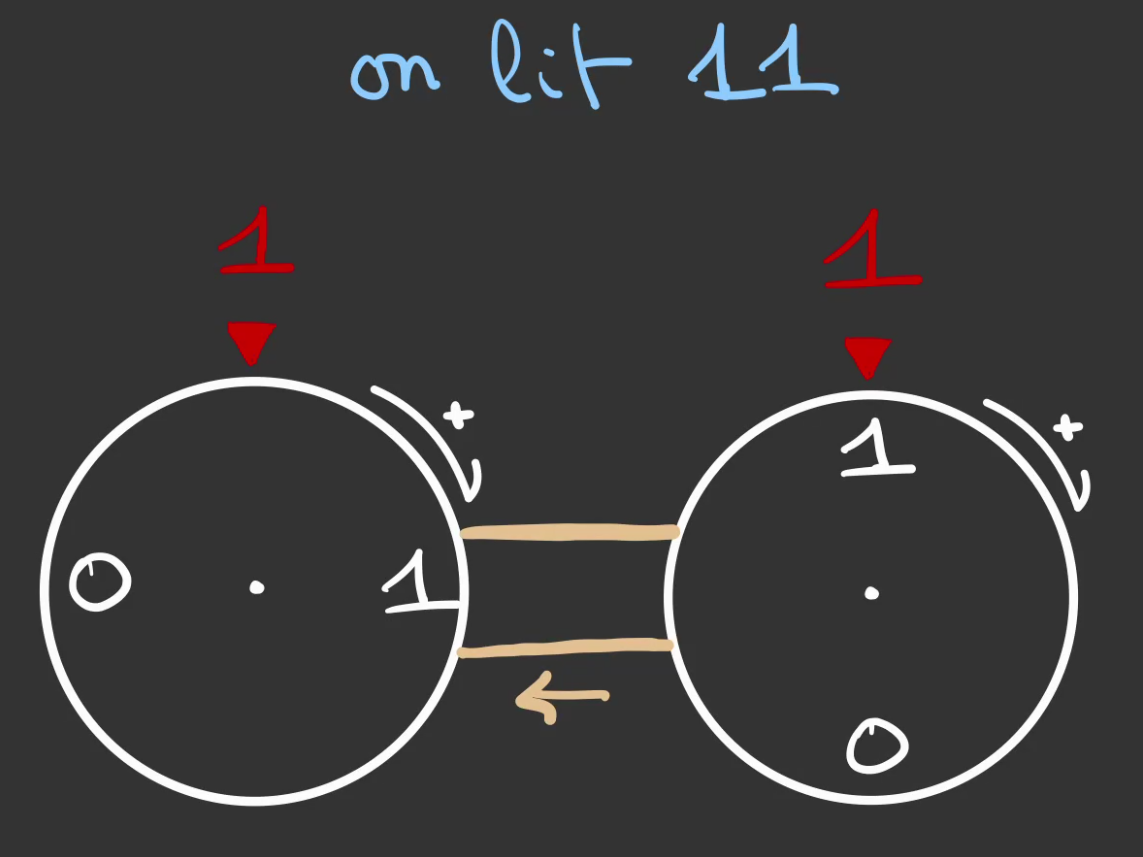
On prend deux roue identique, et on relie la roue de gauche avec celle de droite.
A l'état initial, les deux roues sont à 0. On lit 0.
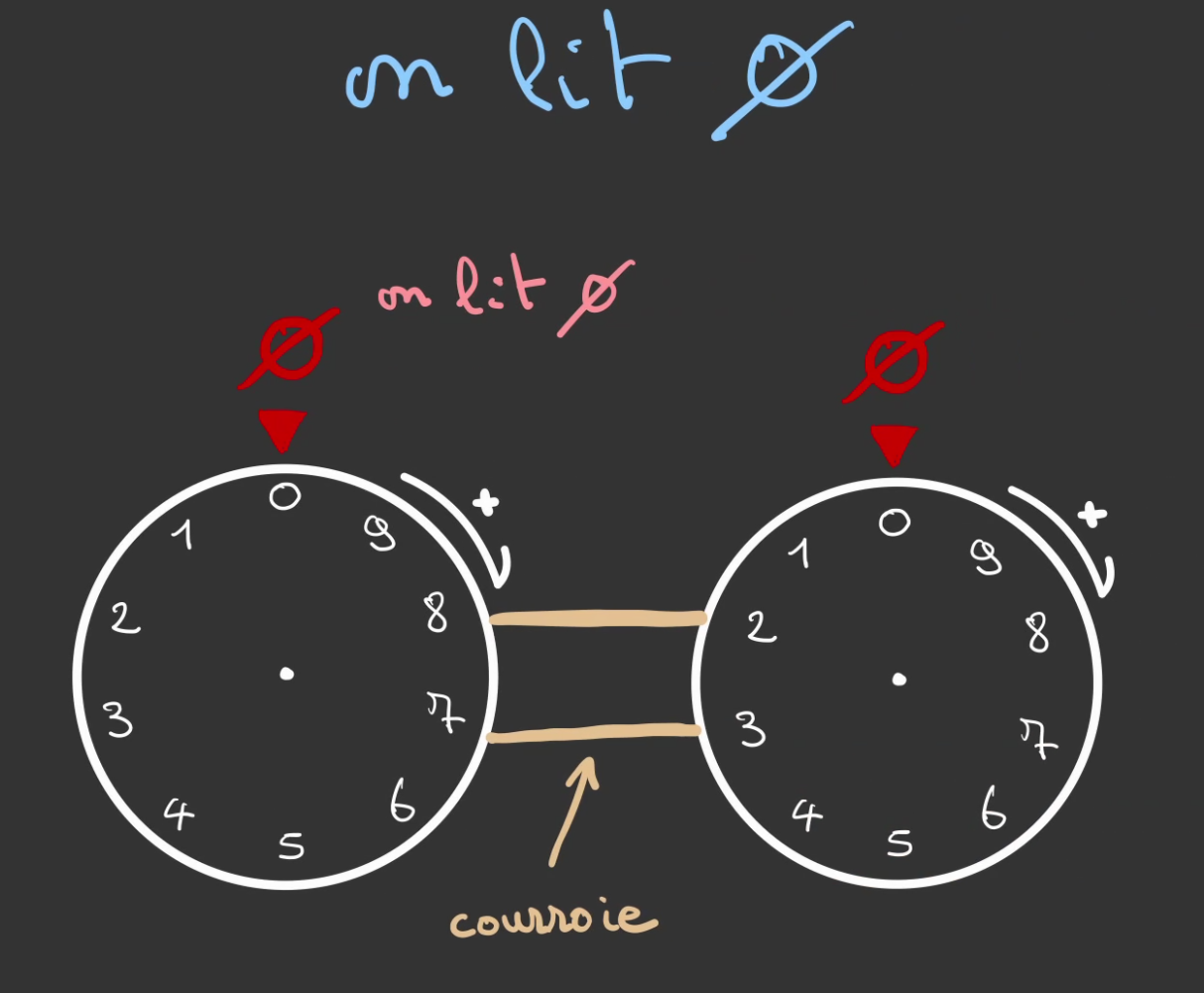
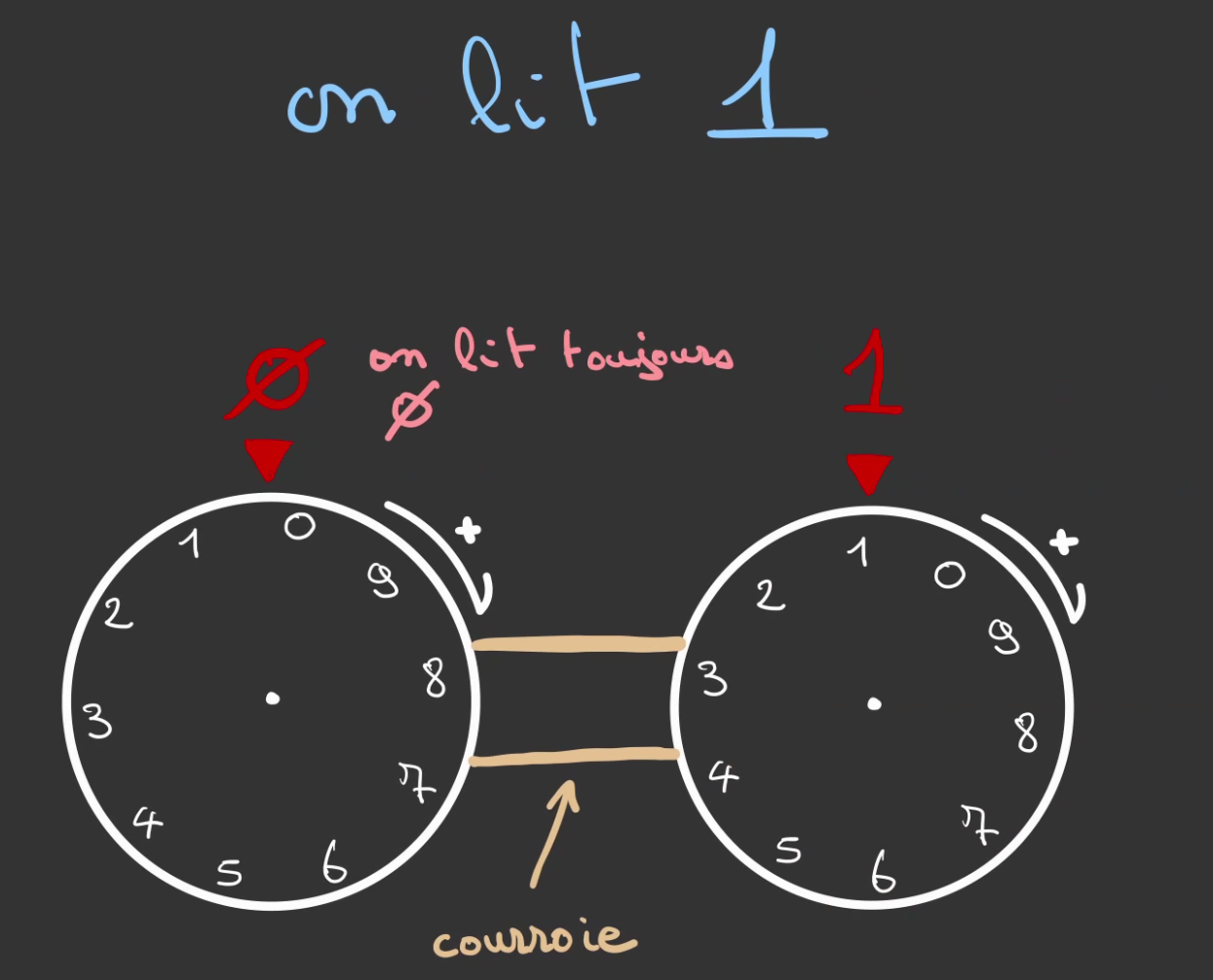
Si on effectue on tourne de 1 graduation la roue de droite.
La roue de gauche entraînée par la courroie, tourne de 1/10 de graduation.
On lit alors 1 sur la roue de droite et quelque chose entre 0 et 1 sur la roue de gauche.
Mais que l'on considère comme valant 0.
En lisant les deux valeurs de roue on se retrouve avec "01" que l'on interprète comme un 1.
Revenons à la situation où la roue de droite est à 9.
La roue de gauche est presque sur le 1, mais pas totalement.
Elle est donc toujours à 0.
On lit "09" donc 9.
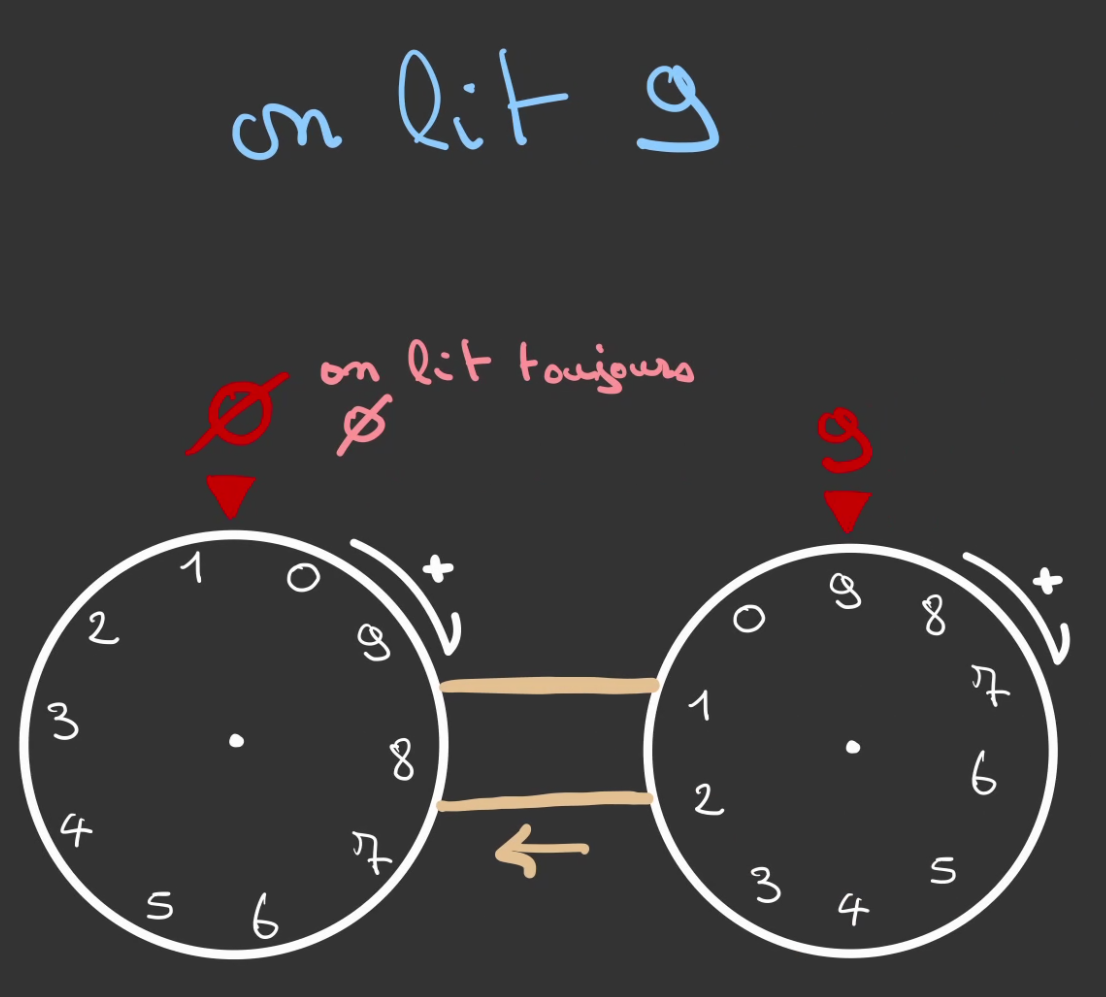
On avance d'une dernière graduation la roue de droite, qui évidemment revient à 0. Mais la courroie entraîne une dernière fois la roue de gauche.
Qui finit par afficher 1.
On lit alors "10" ou 10.
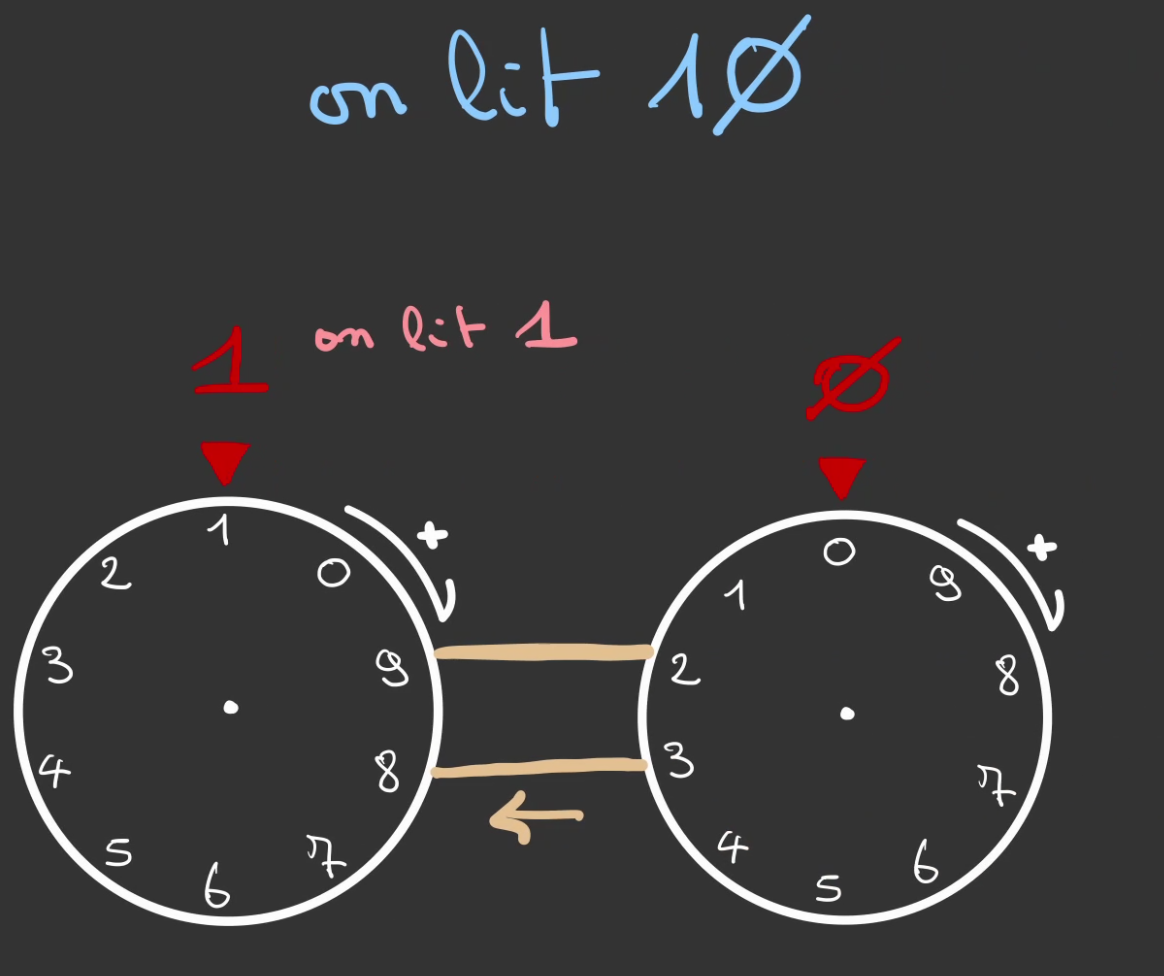
Ça y est, nous pouvons aller plus loin que 9. 🤩
On peut alors continuer à incrémenter jusqu'à 11.
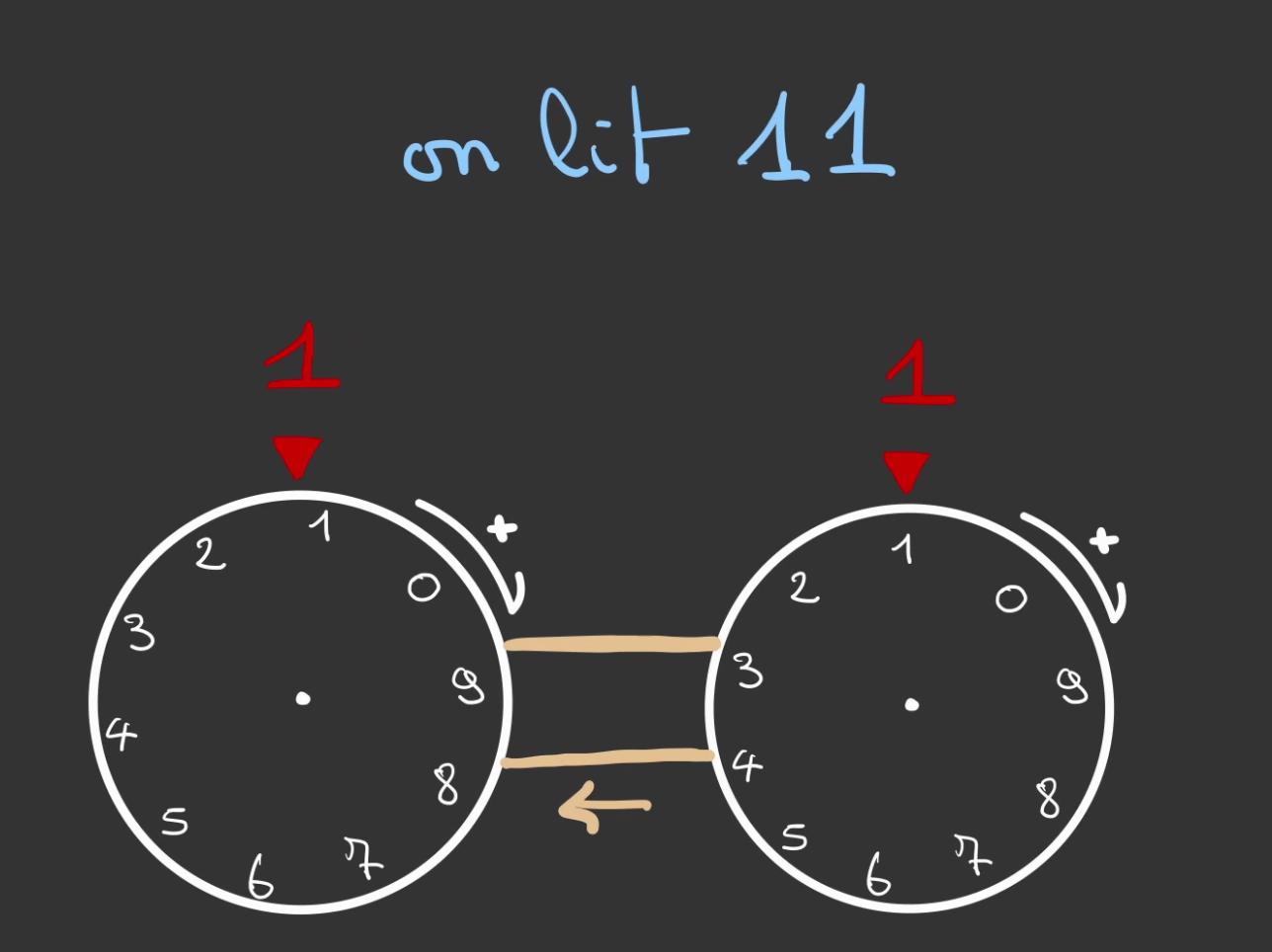
Ou même 19.
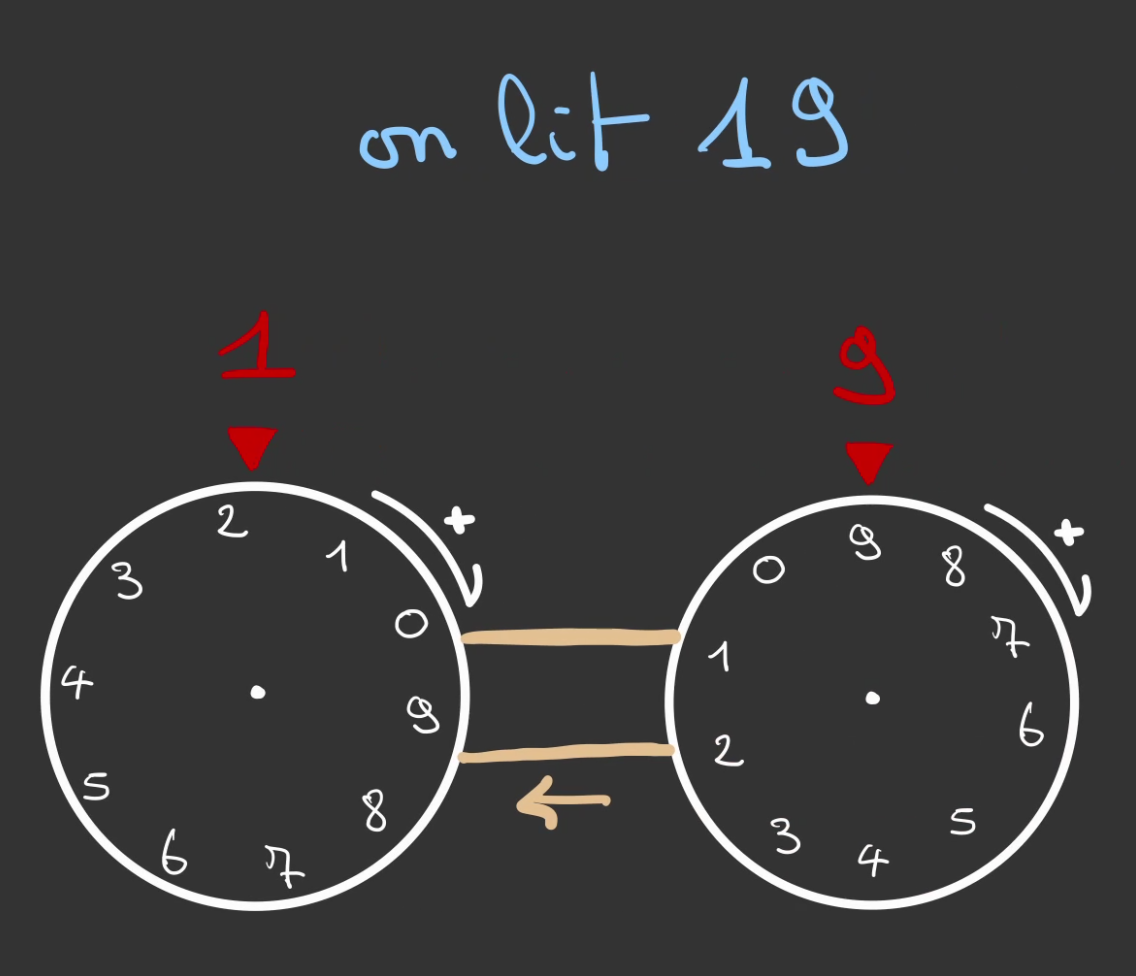
À 19, une incrémentation supplémentaire nous fait passer à 20.
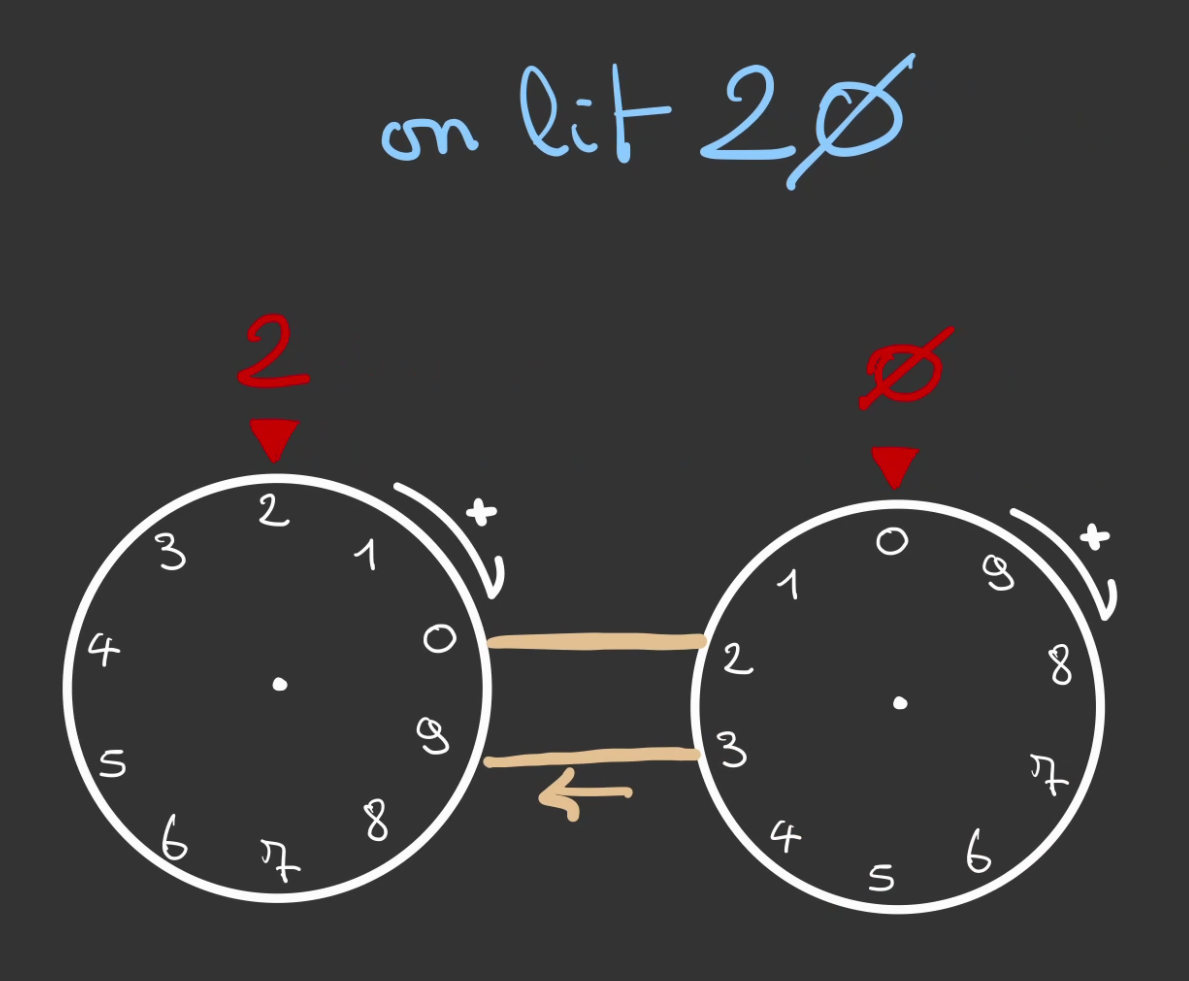
Continue, jusqu'à 99.
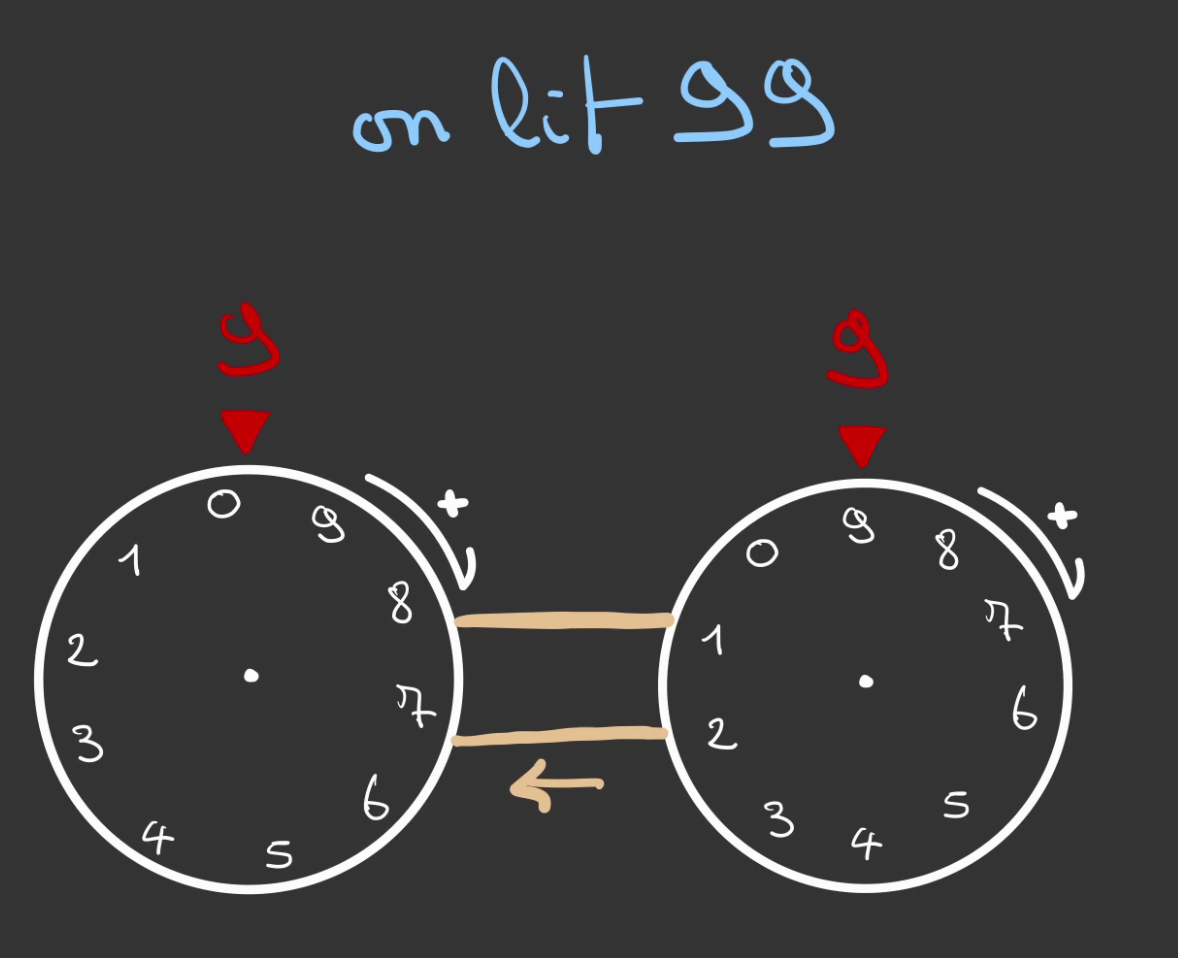
Si on ne fait rien, on se retrouve devant le même problème que l'enfant qui recommençait à 1 après 10.
Nos roues, reviennent à leur état initial.

Du coup la solution est donc de rajouter une roue.
À 99, cela donne ça:
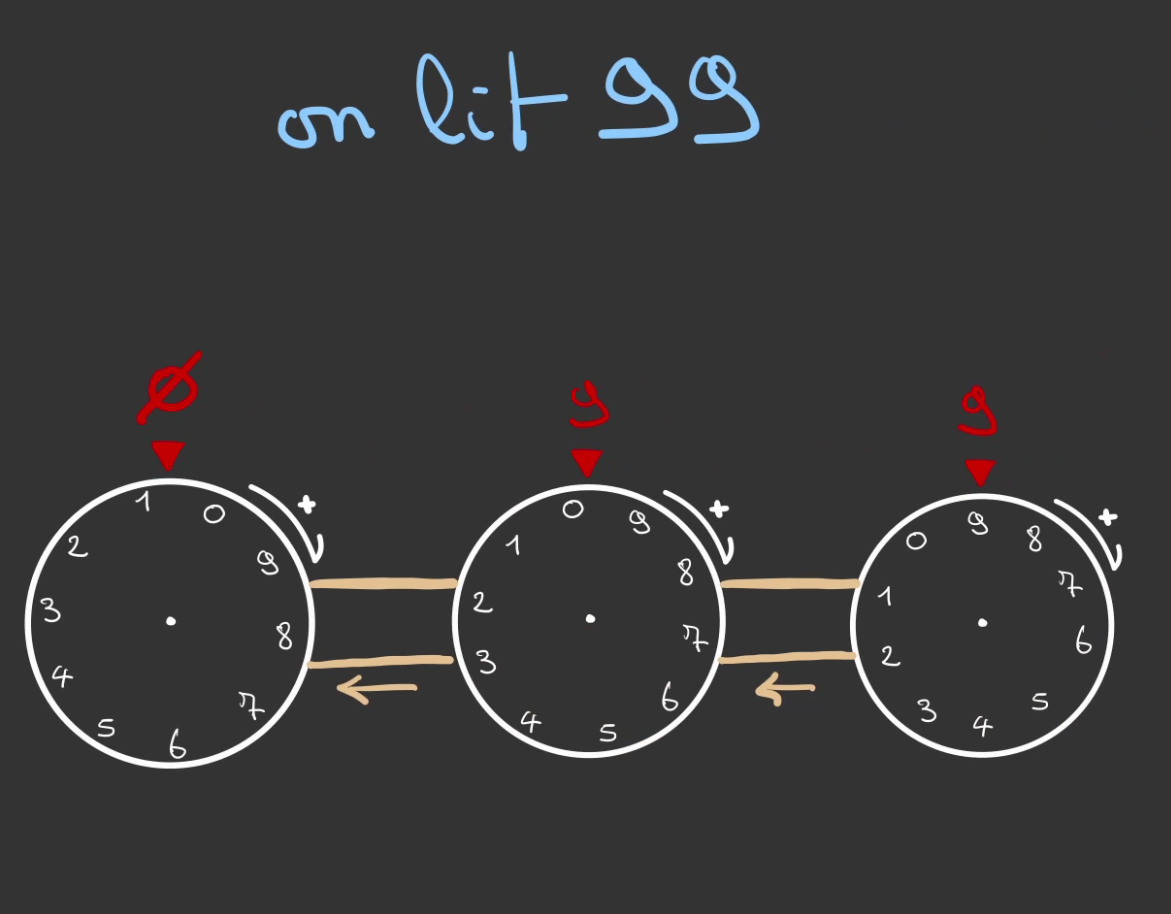
À 100, ceci:
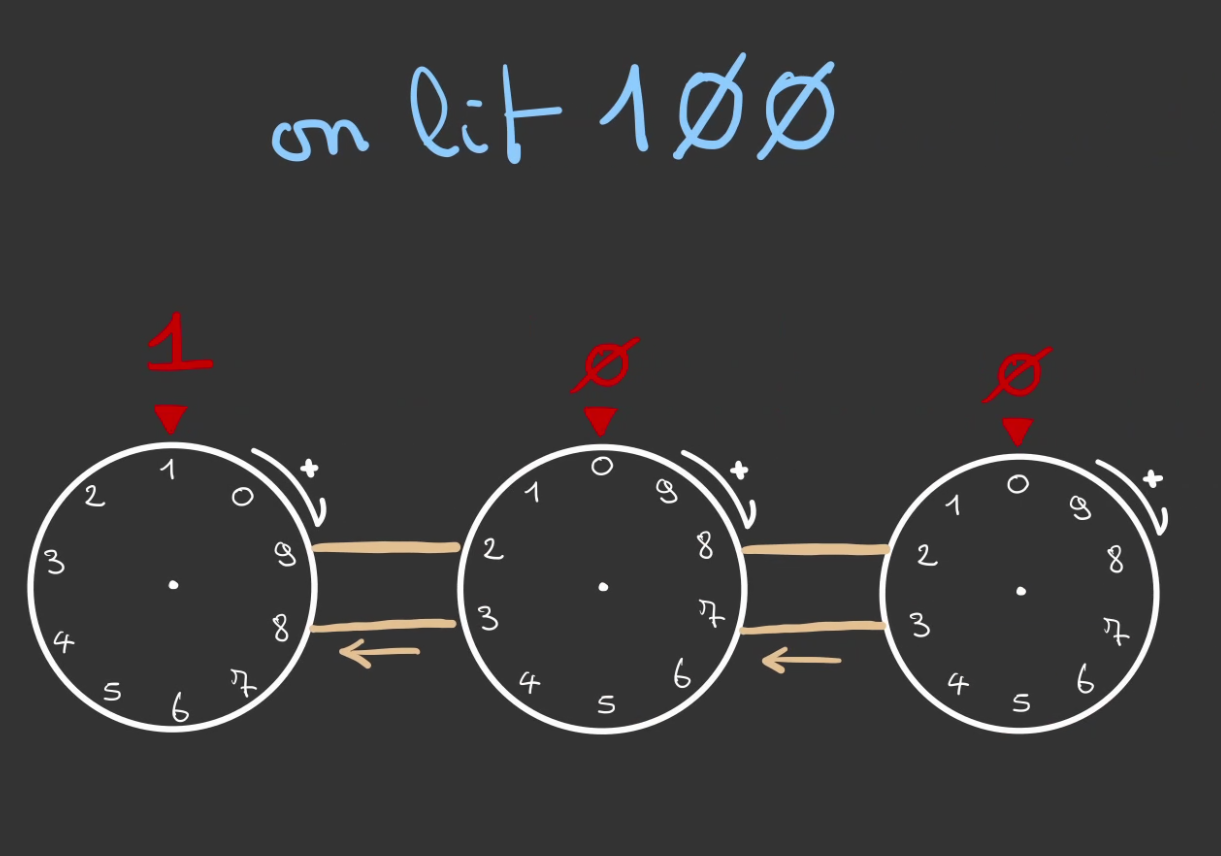
On peut rajouter autant de roue que l'on souhaite pour représenter des nombres de plus en plus grands.
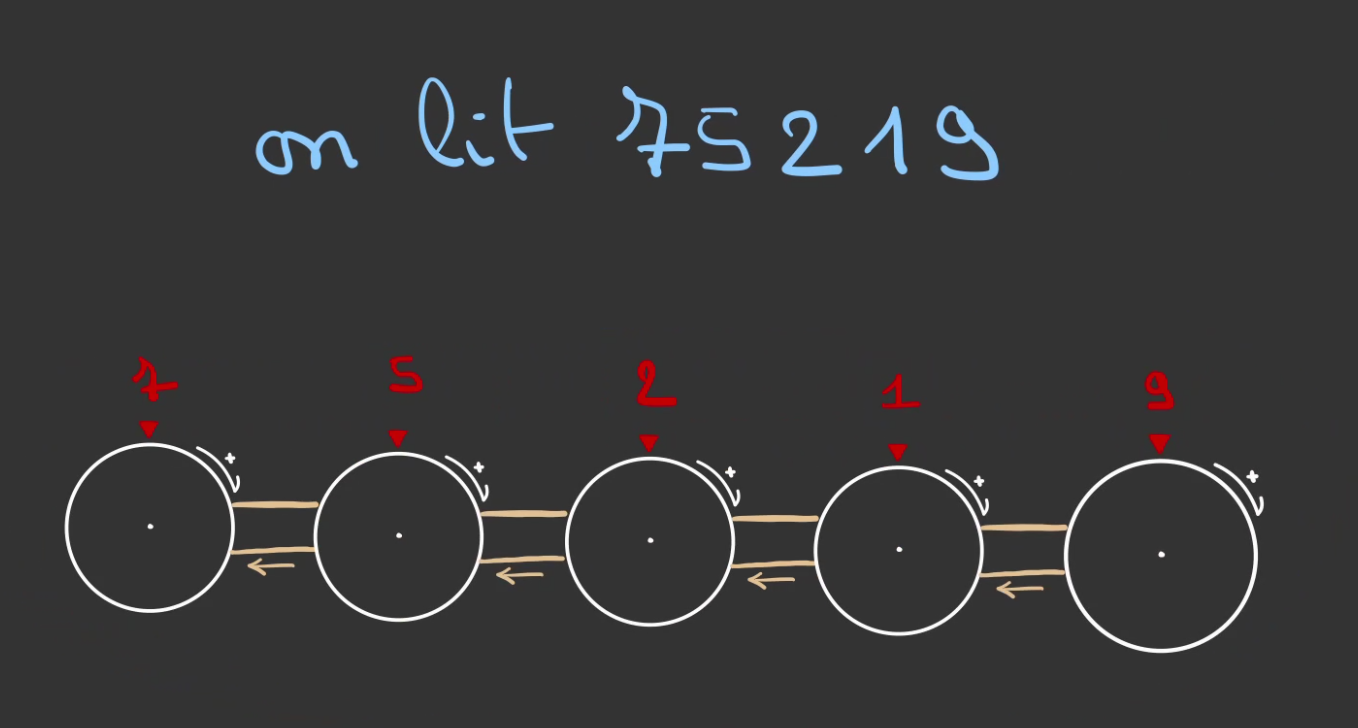
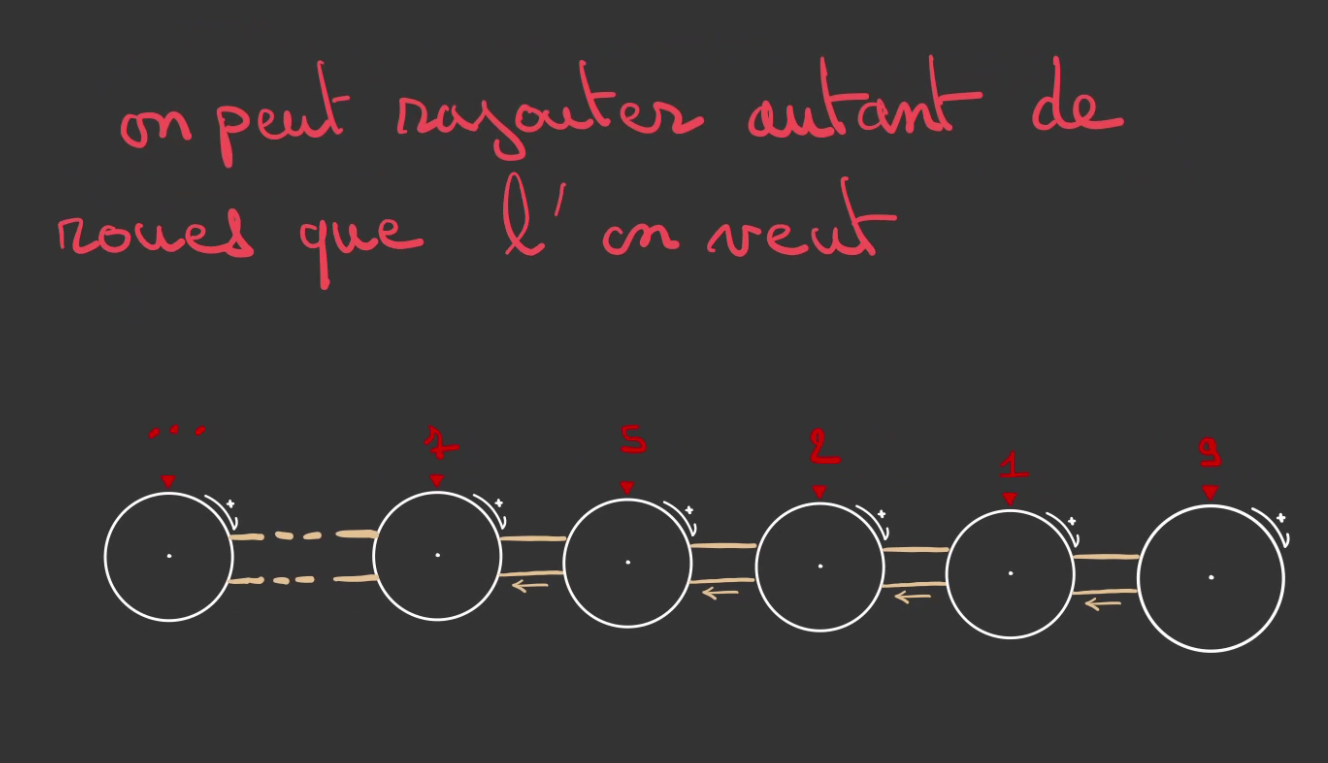
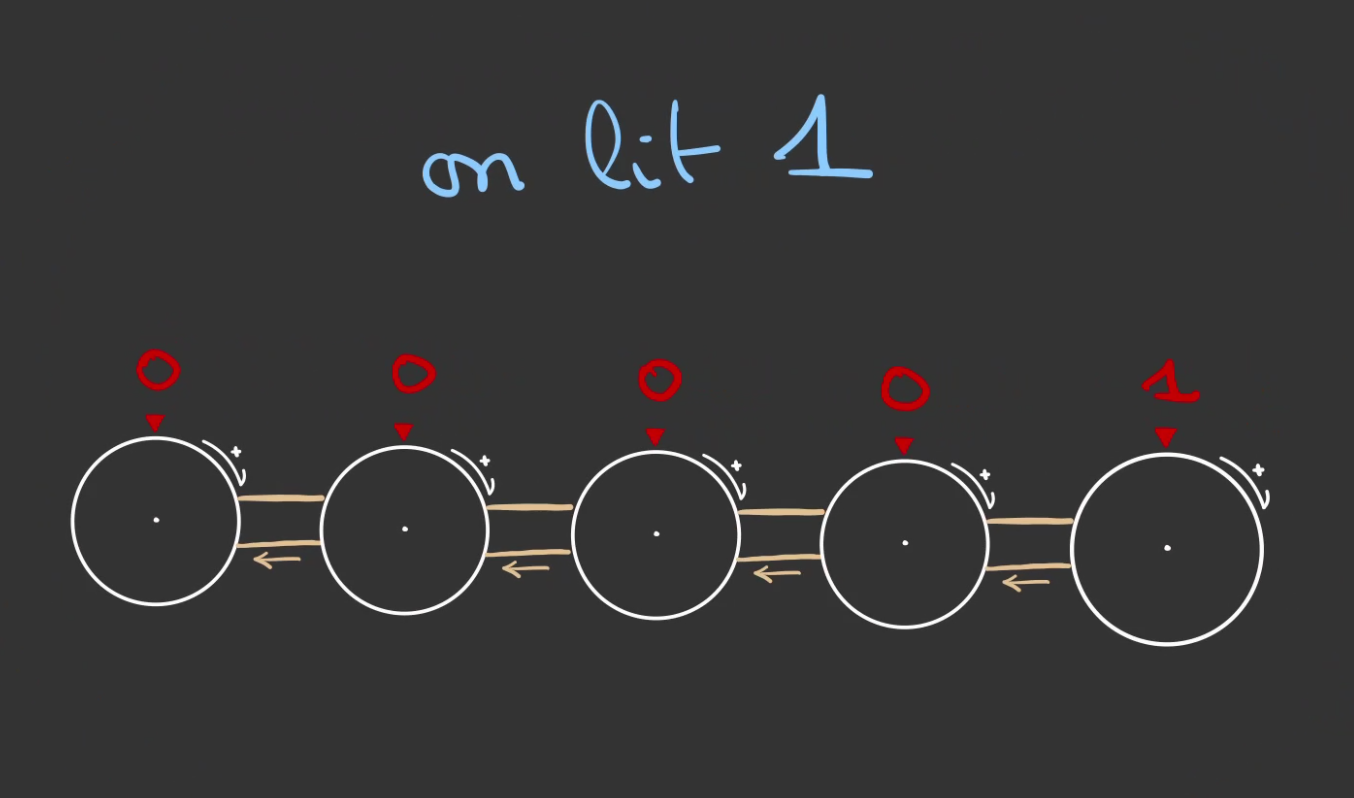
Un nombre très petit peut être représenté sur un très grand nombre de roues, il suffit de mettre les roues à la gauche du nombre à 0.
On nomme base, le nombre de cran de la roue.
Ici, 10 crans, c'est donc de la base 10.
Cette base a un petit nom, on l'appelle la base décimale.
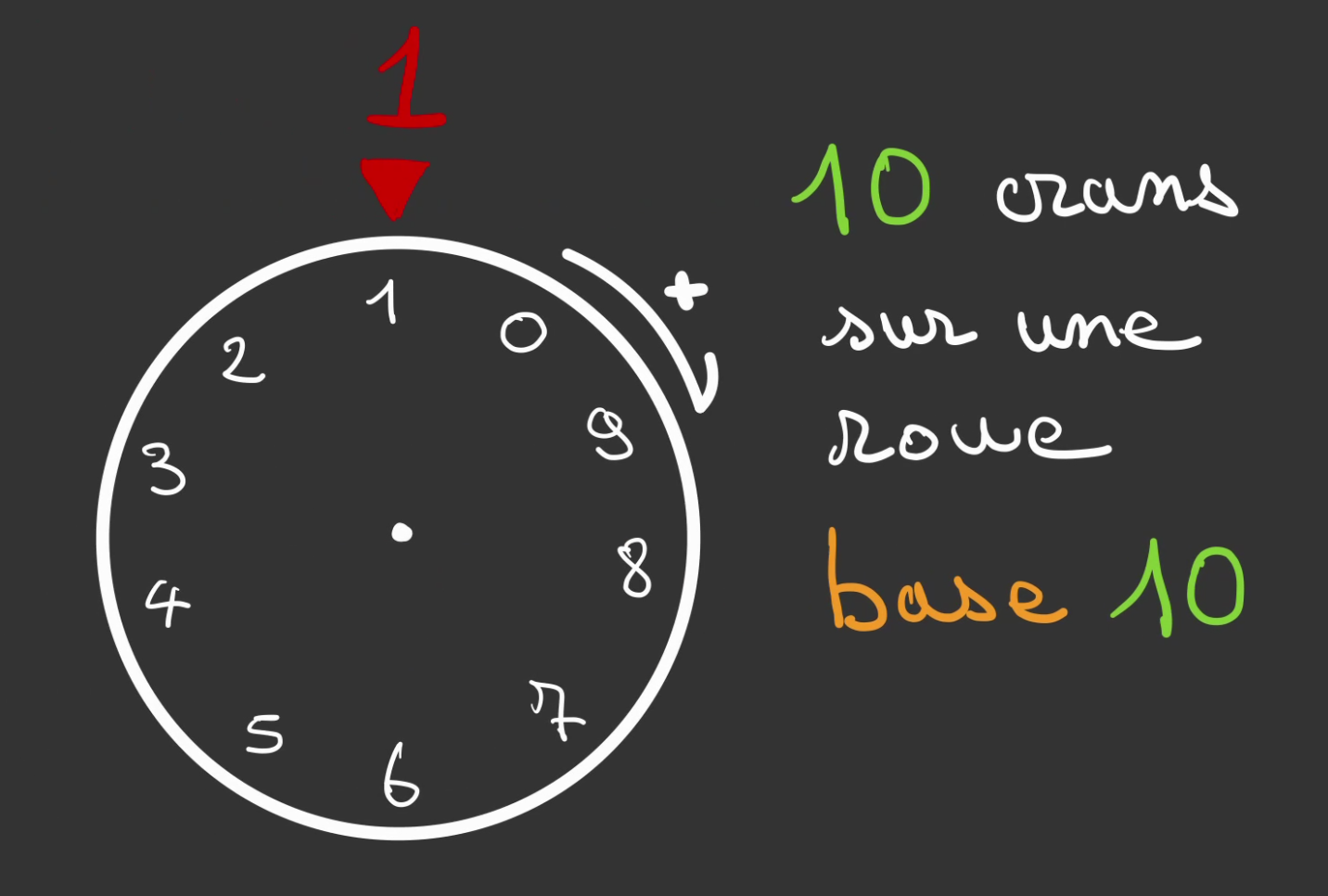
Mathématiques
En primaire, on nous a parlé des dizaines et des unités, et bien c'est le nom que l'on va donner à nos roue.
On va dire que les dizaines sont en rouge et les unités en jaune.
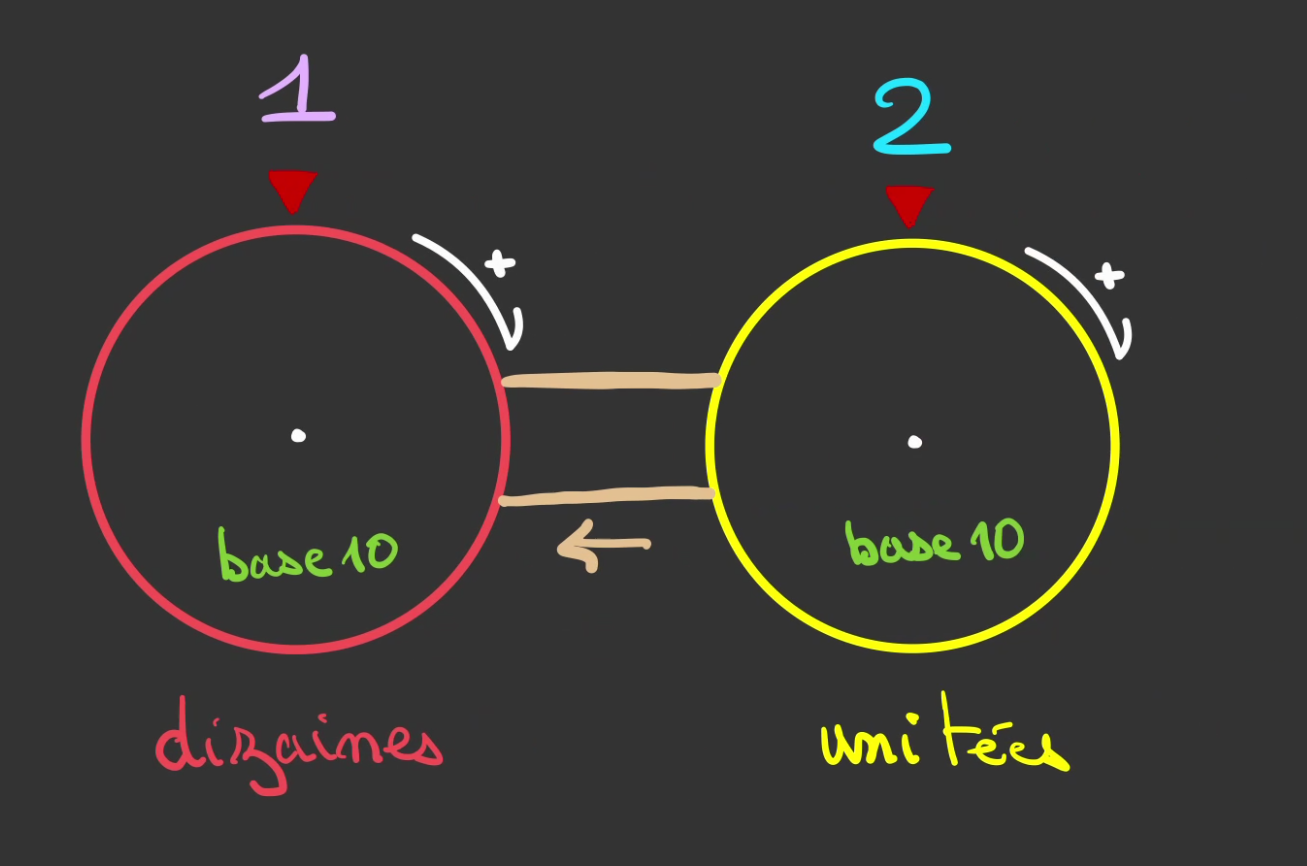
Le nombre en violet "compte" combien de fois la roue jaune à réalisé de tours complets.
C'est en quelque sorte une mémoire.
Nous allons renommer les roues pour plus de simplicité en fonction de leur place en partant de la droite pour aller vers la gauche.
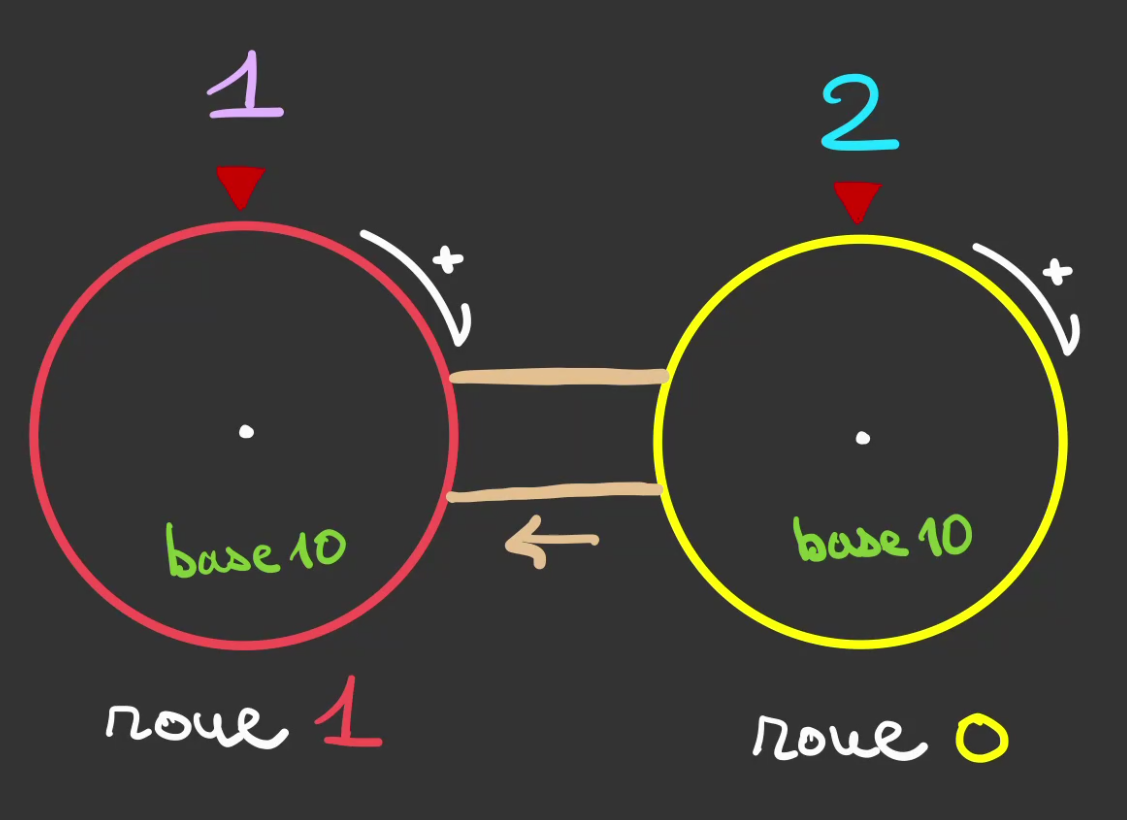
Il y a 10 graduation sur la roue 0, 1 graduation de la roue 1 équivaut donc à 10 graduations de la roue 0.
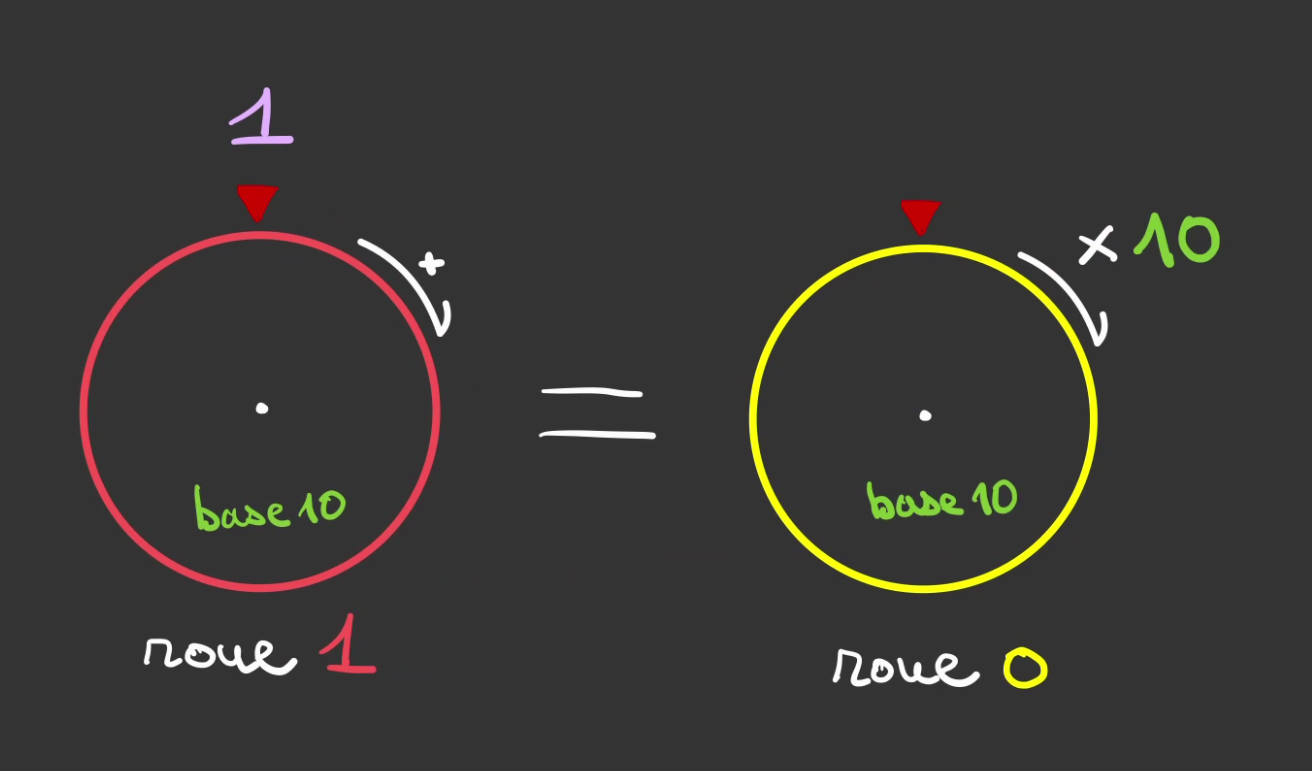
On introduit une nouvelle notation:

Puis on utilise les puissance de 10 pour généraliser l'écriture.
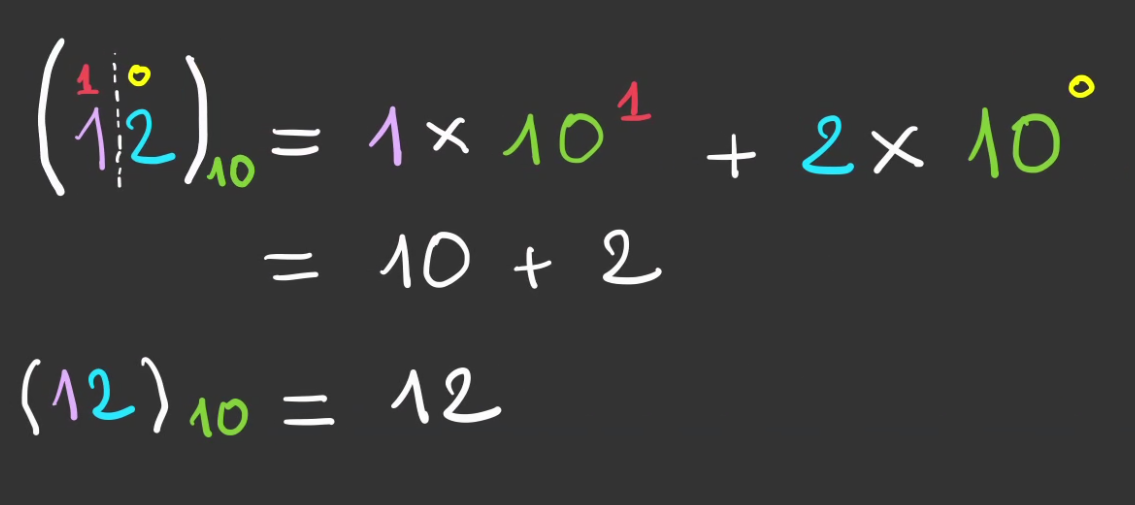
Si l'on a plus de roues, le principe reste identique
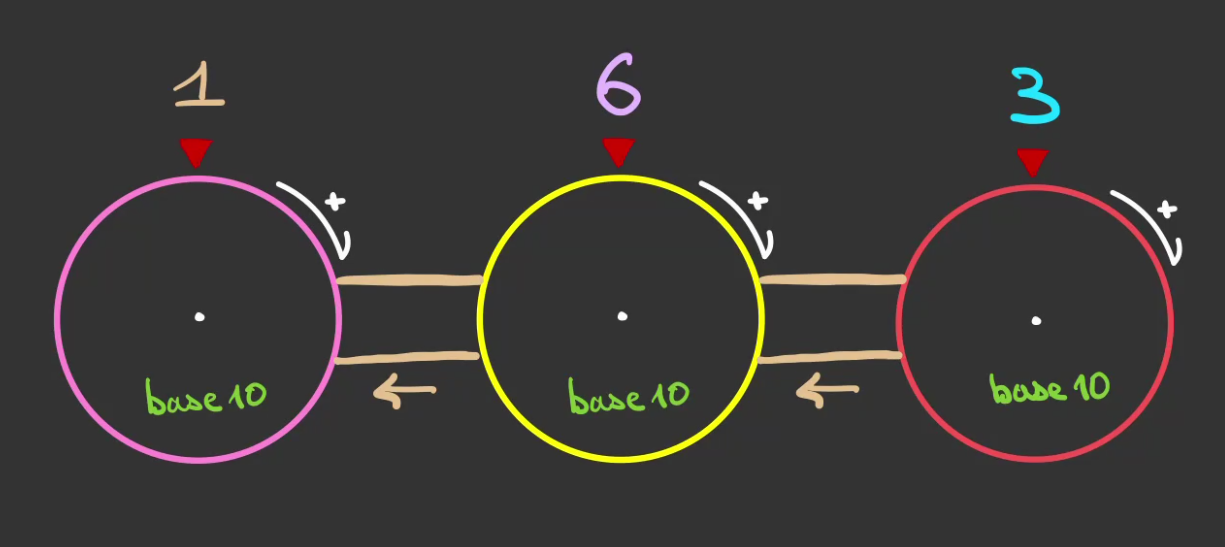
Que l'on décompose en
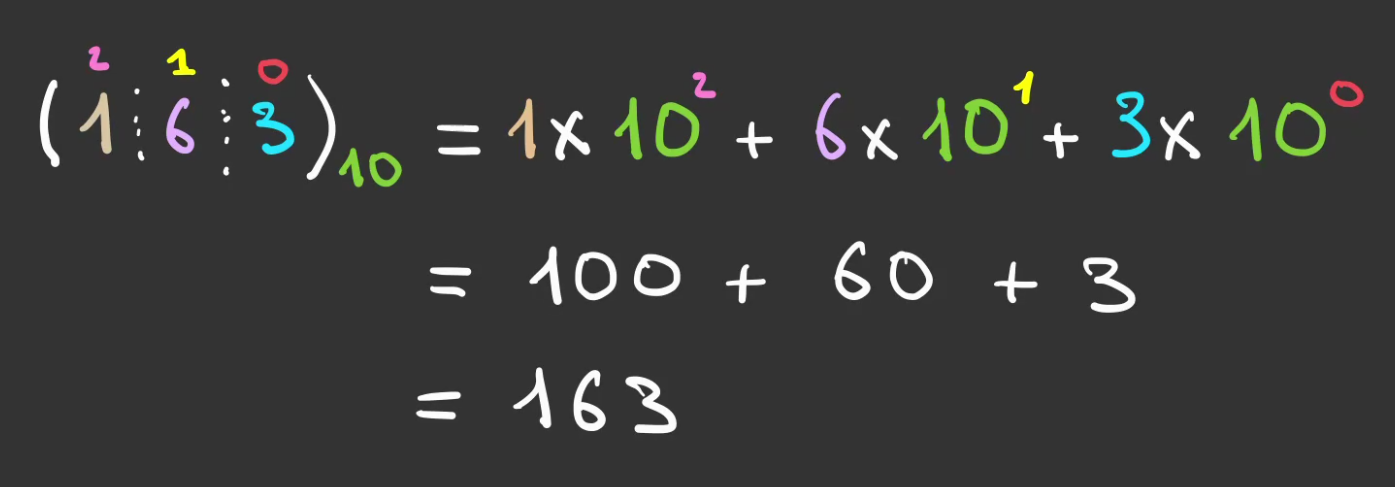
base 2
Il est tout a fait possible de faire varier le nombre de crans de la roue.
Si l'on n'a que 2 crans, on passe en base 2, ou plus généralement appelée binaire.
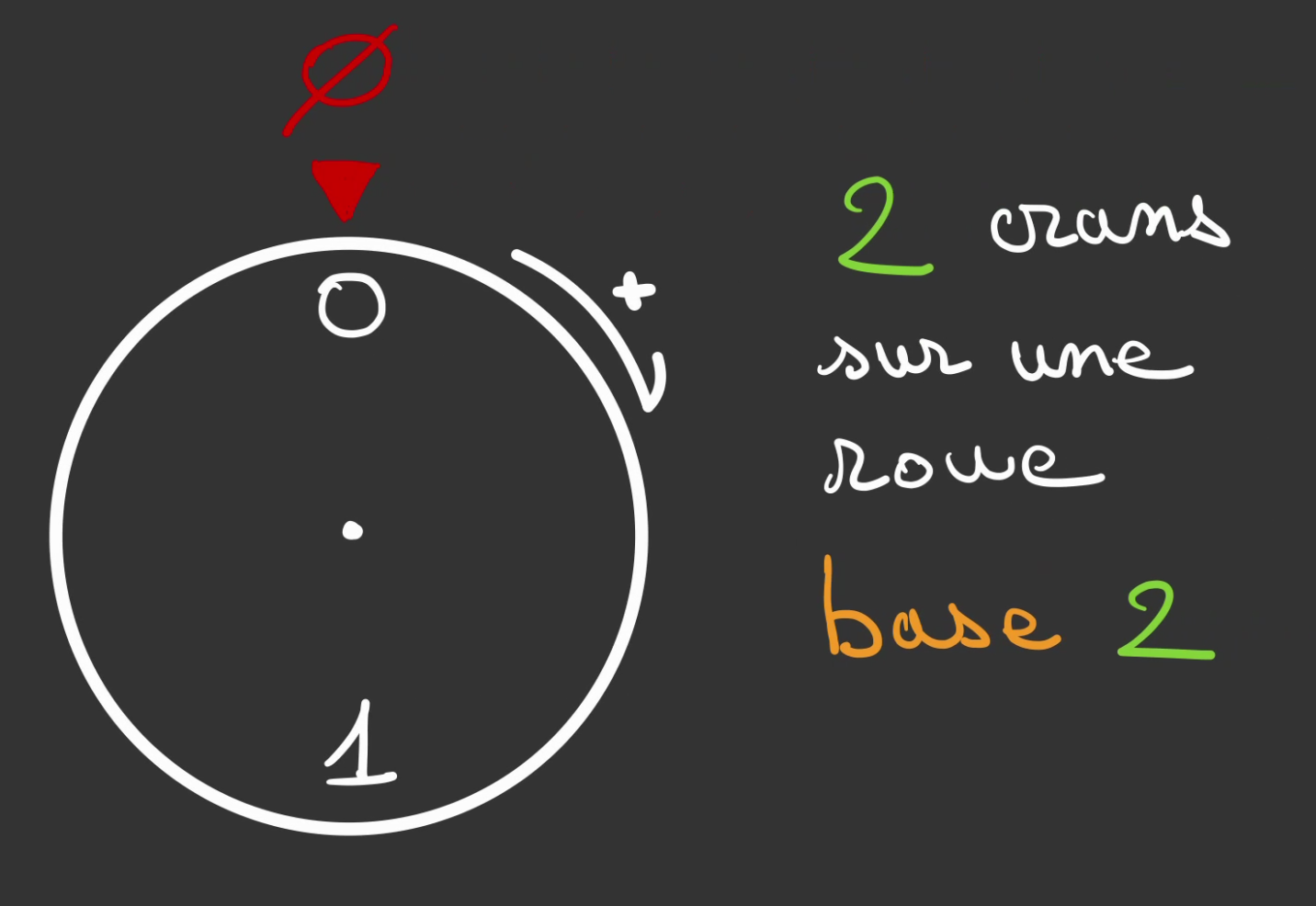
Cela fonctionne de la même manière.
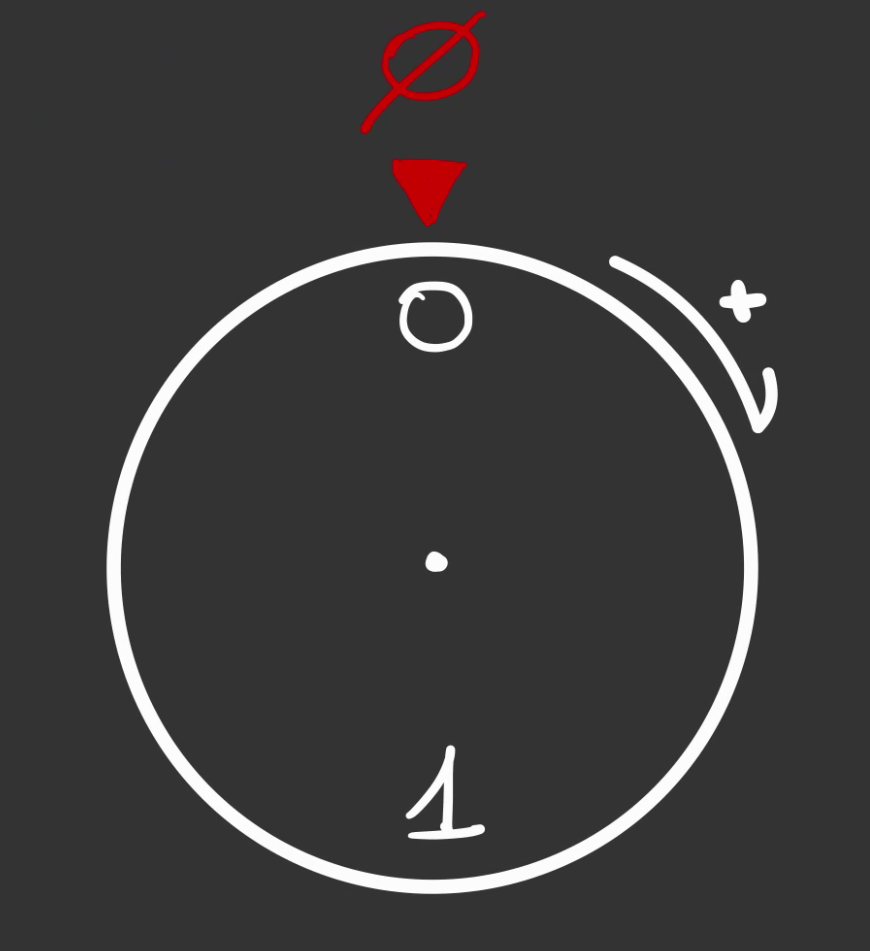
Une roue graduée, chaque graduation faisant un demi tour.
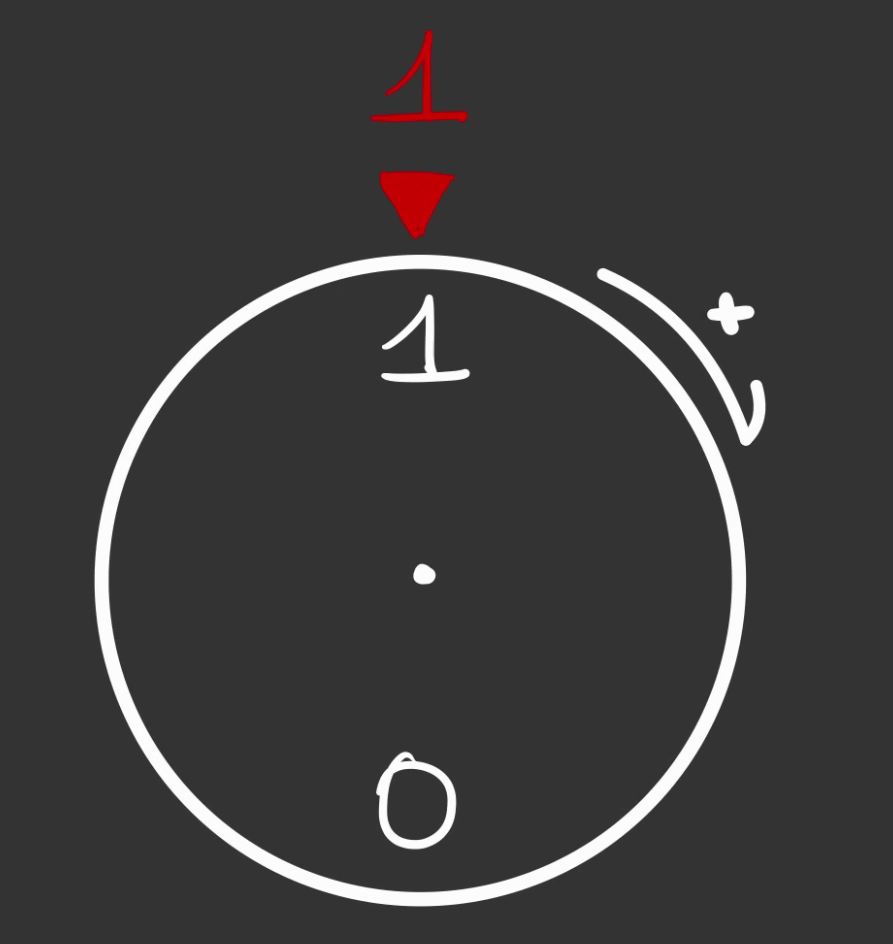
Si l'on fait un tour complet, on se retrouve à l'état initial.

Pour palier le soucis on rajoute une deuxième roue à deux graduations.
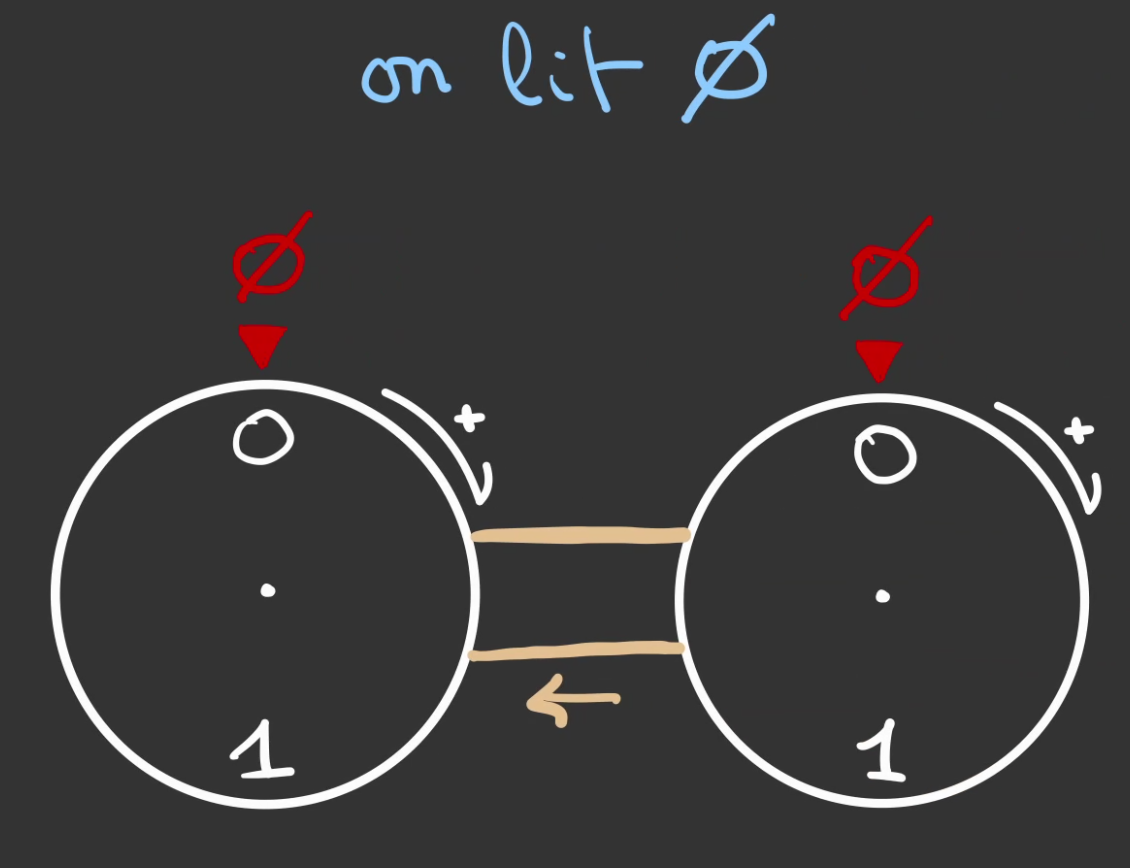
Et on recommence.
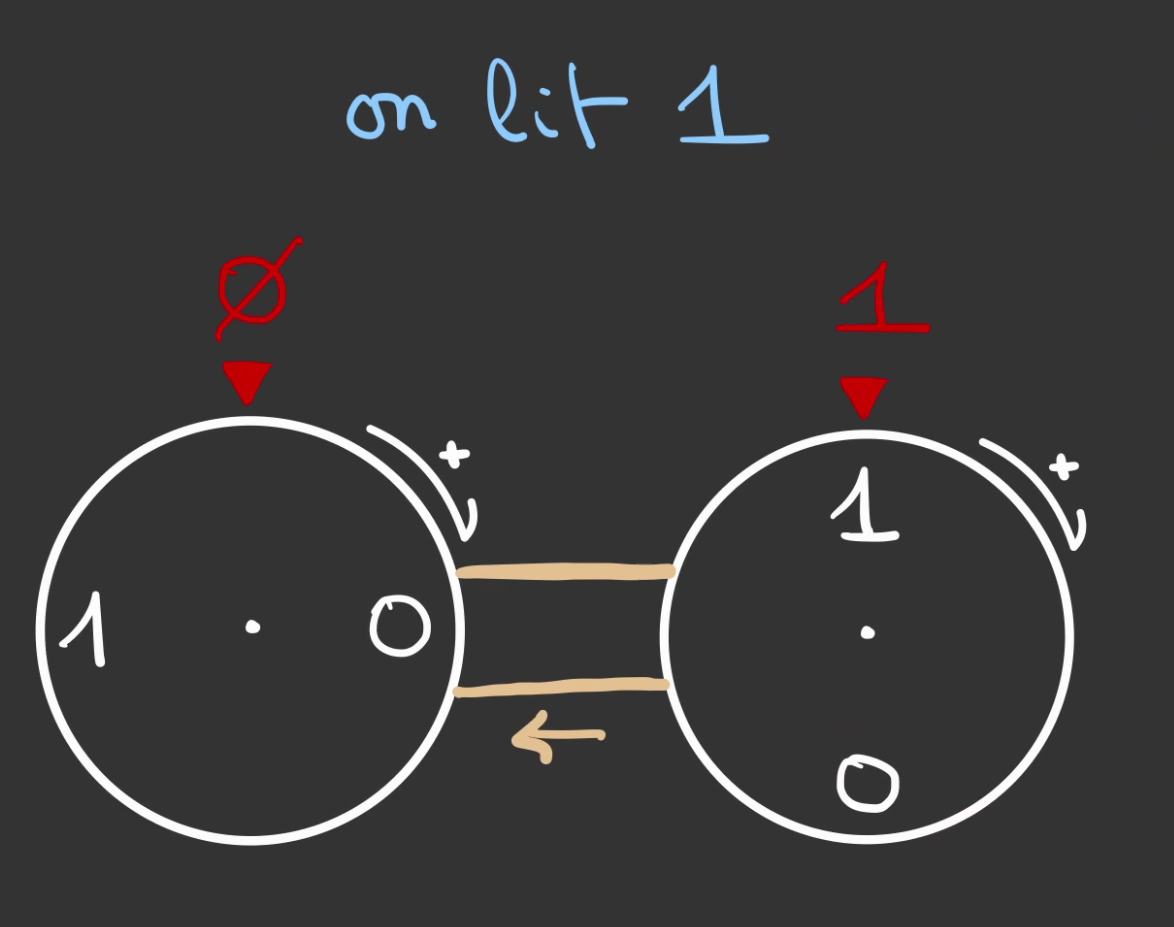
En parrallèle, on fait tourner une roue décimale.

On peut alors décaler d'une graduation supplémentaire sans perdre le compte.
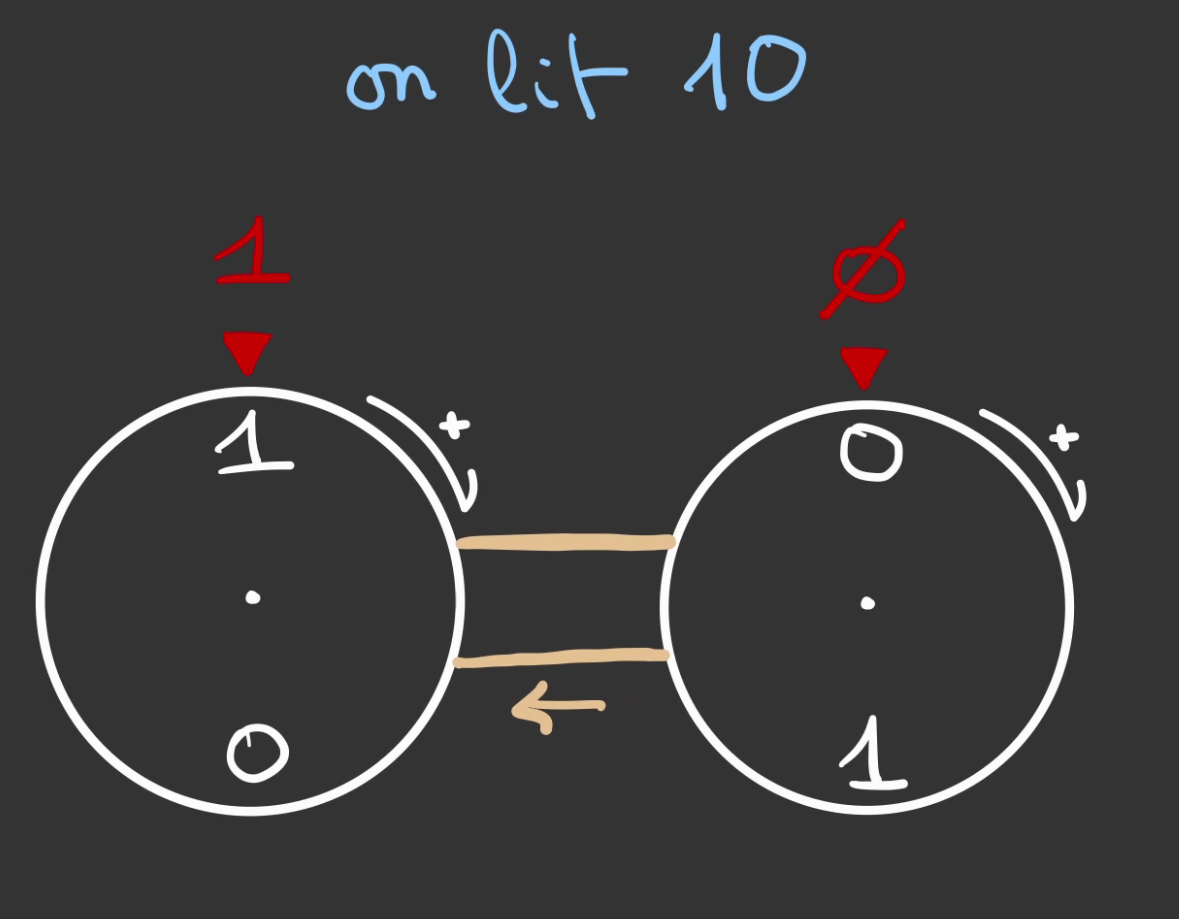
Dans le même temps, notre roue décimale affiche
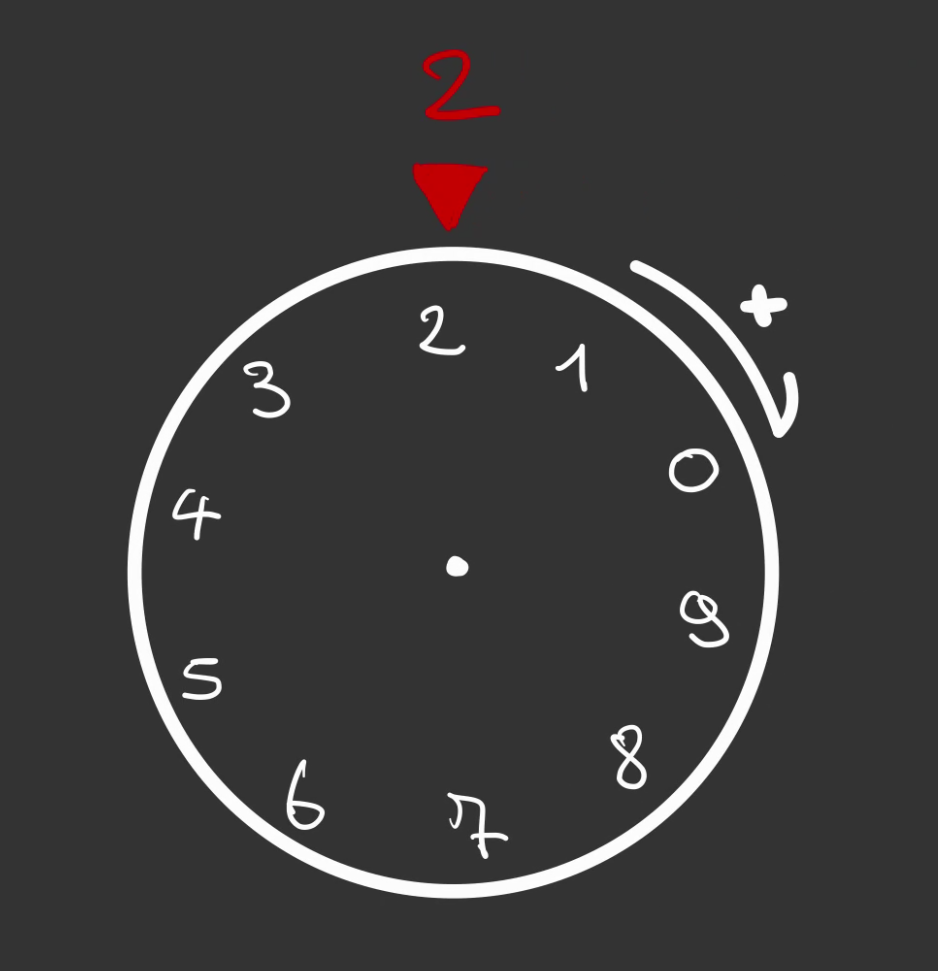
On continue, la roue de gauche se déplace encore d'un quart de tour.
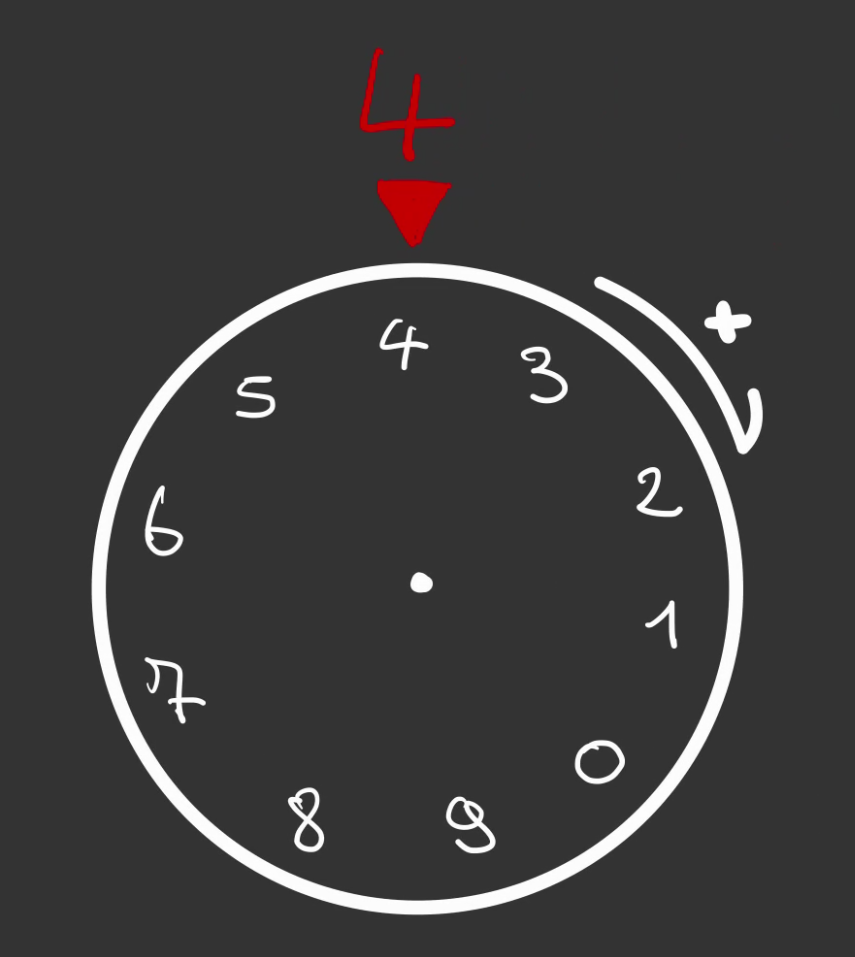
Nous arrivons à 3 sur la roue décimale.

Encore une graduation à gauche et "00". 😥

Alors que l'on a 4 sur la roue décimale.
On rajoute une roue. Pour être dans la capacité de représenter "4".
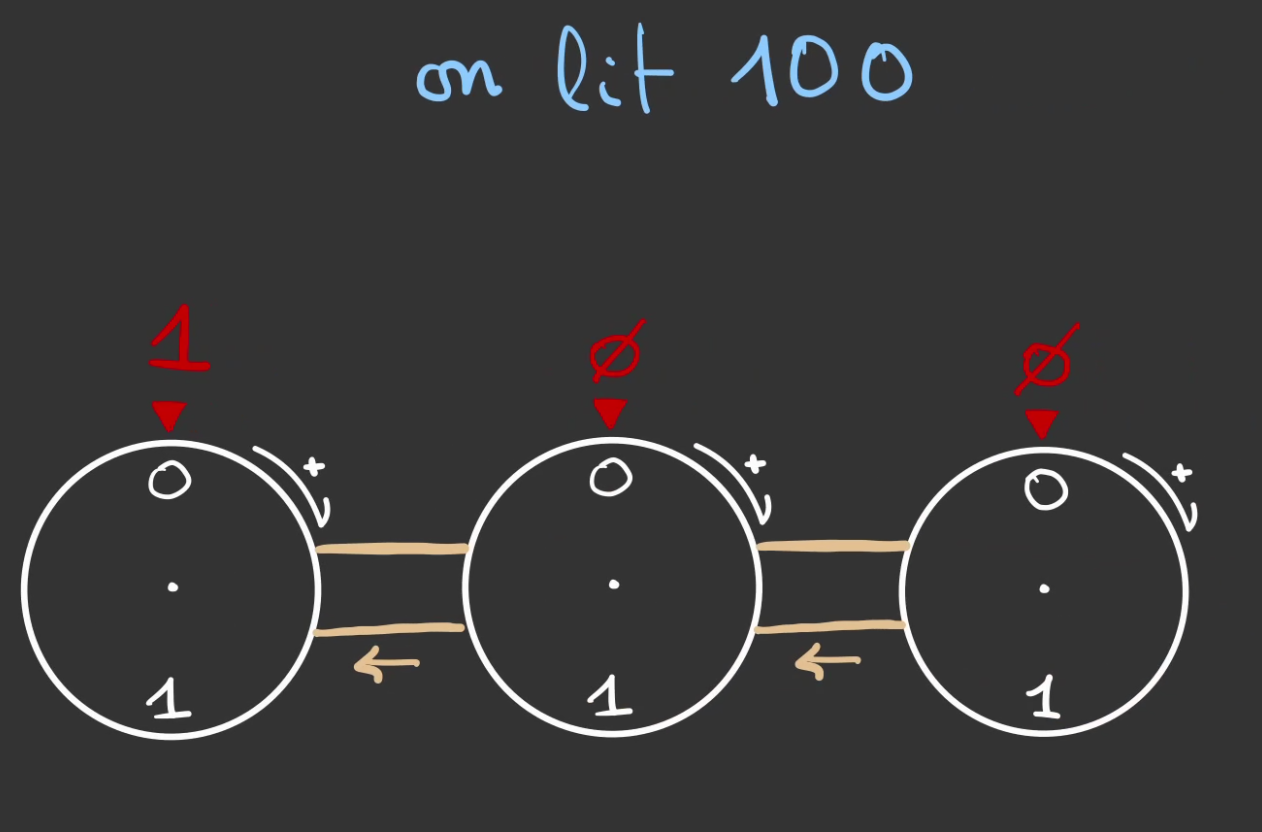
Mathématiques
Faisons tourner la roue une dernière fois. On obtient 5 en base 10.
On renomme nos roues des bits.
Et l'on numérote comme l'on a pu le faire en base décimale.
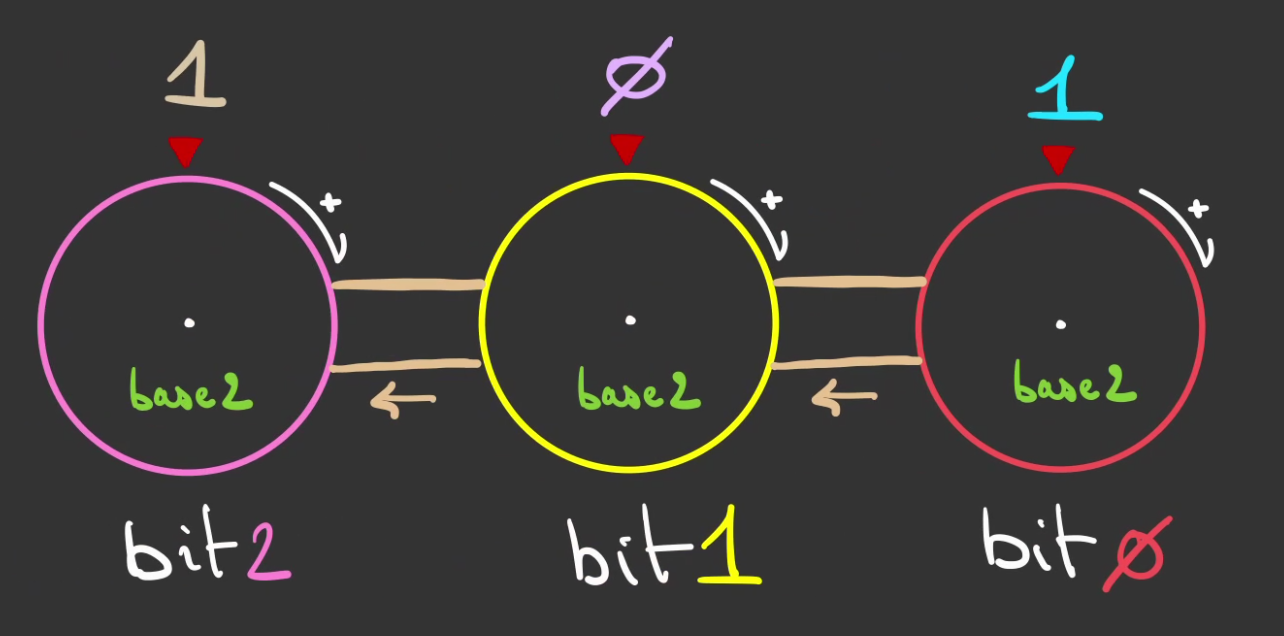
On peut alors réutiliser notre notation.
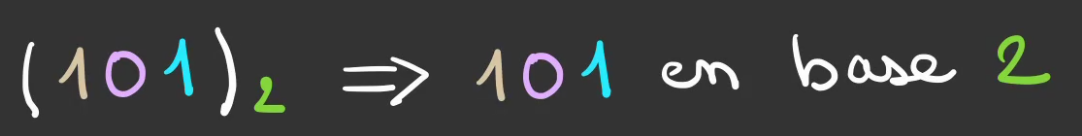
Cette fois-ci, il faut faire tourner 2 fois la roue 0 pour décaler d'une graduation la roue 1.
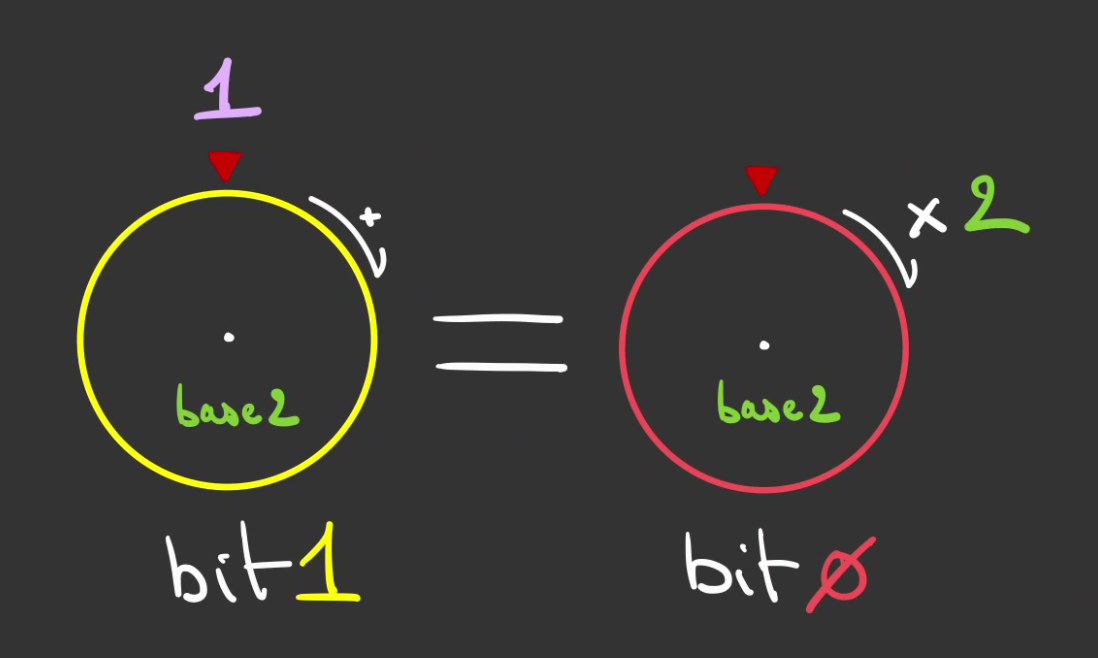
Il est alors possible de réaliser la décomposision cette fois-ci en puissance de 2.
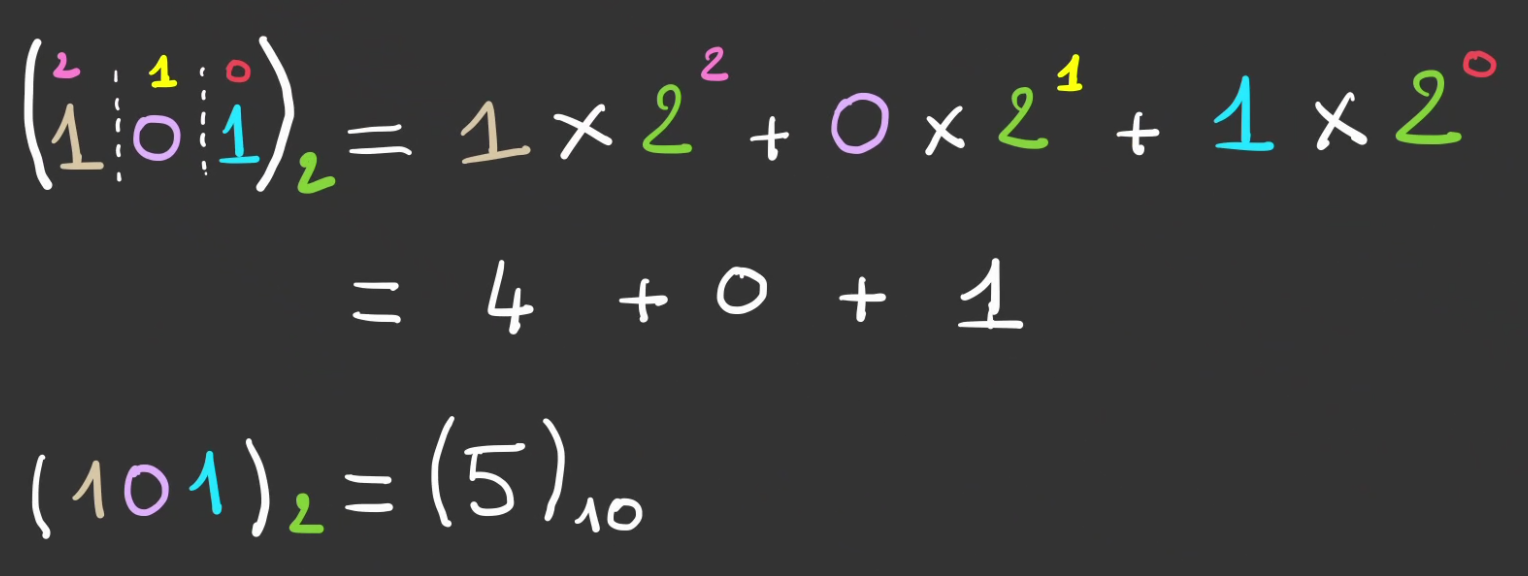
Ce qui se généralise très bien.
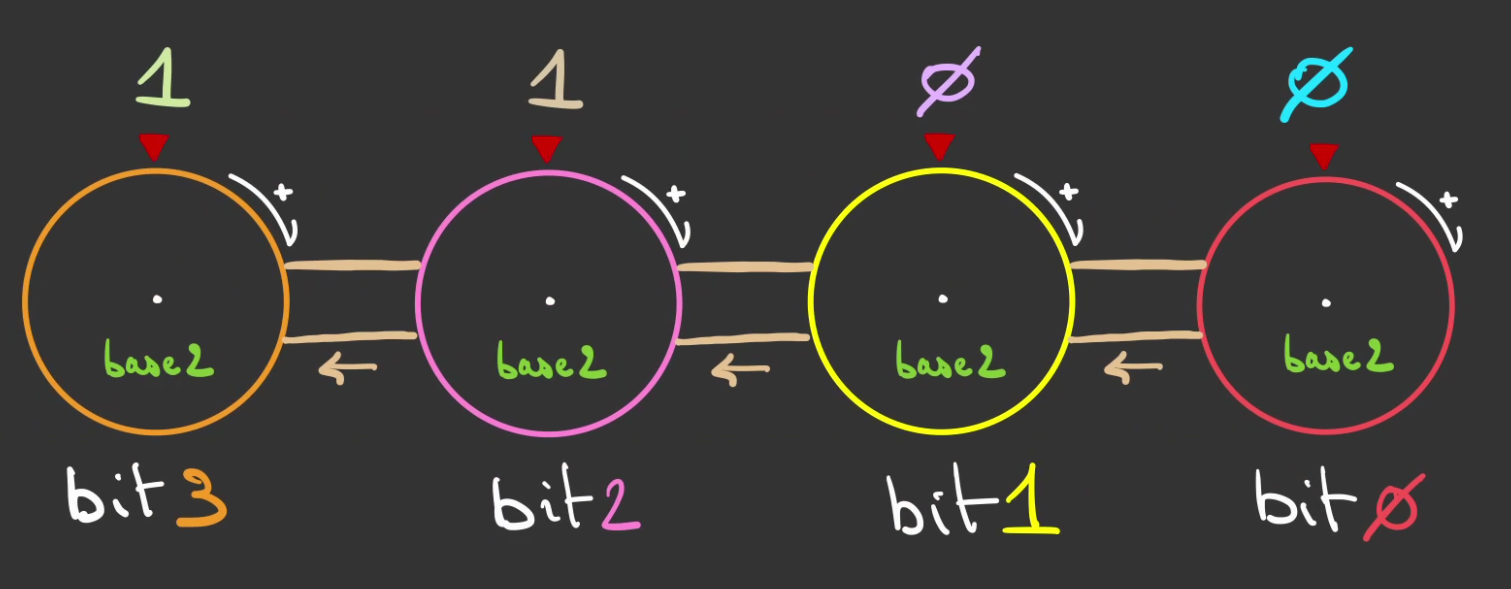
En
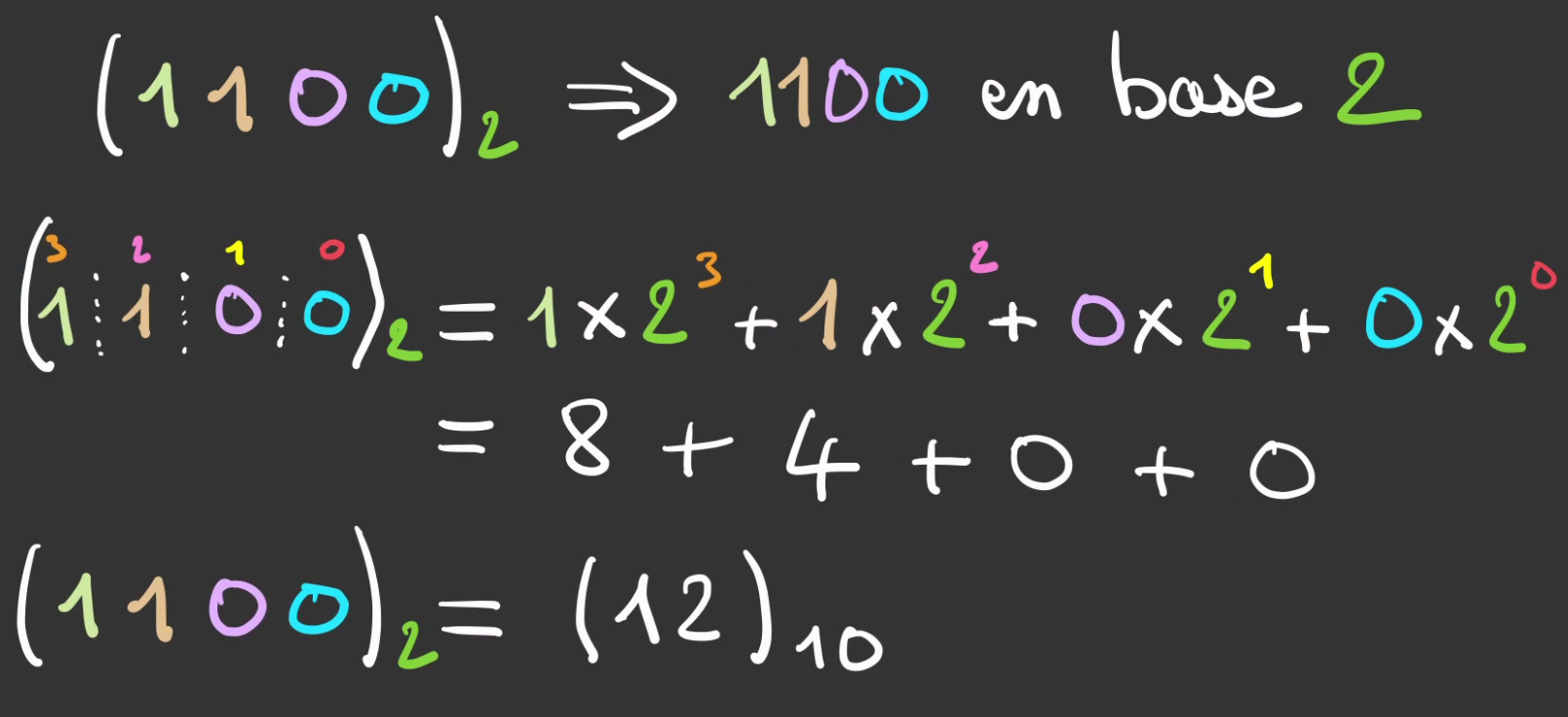
Ce nombre est généralement noté en informatique 0b1100.
Base 16
Maintenant que l'on est rodé, on peut jouer avec la définition des bases.
On peut par exemple rajouter des graduation à notre roue et en faire une à 16 graduation.
Comme on n'a plus de chiffres, on passe au lettres.
On nomme cette base 16, la base héxadécimale.
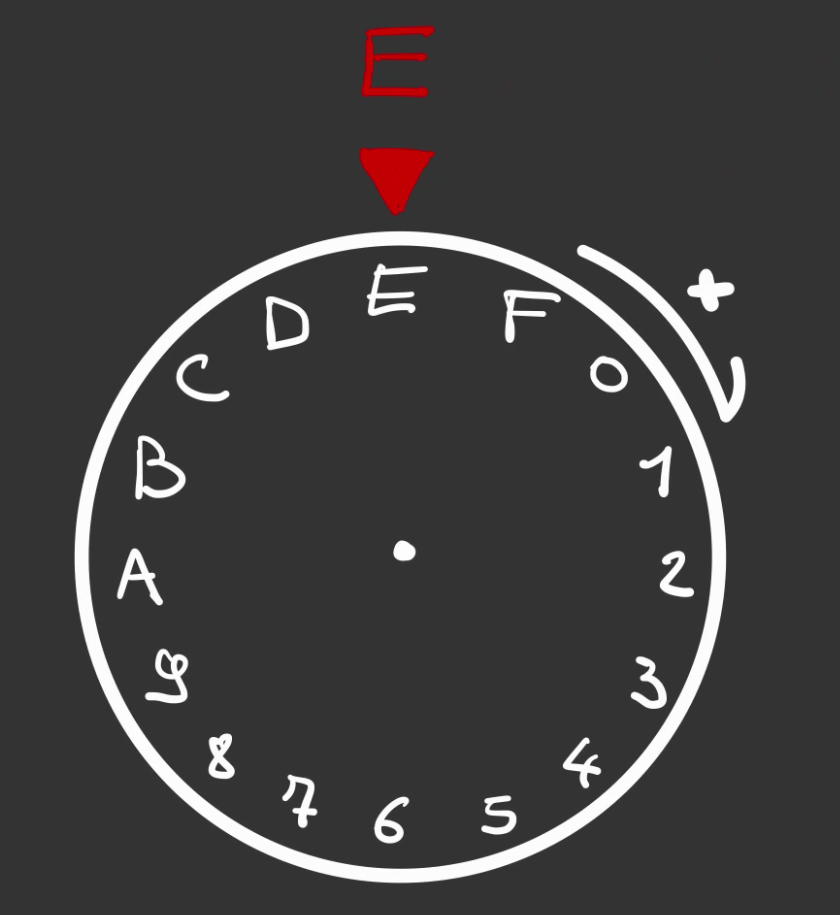
On se créé un nombre héxadécimale A3.
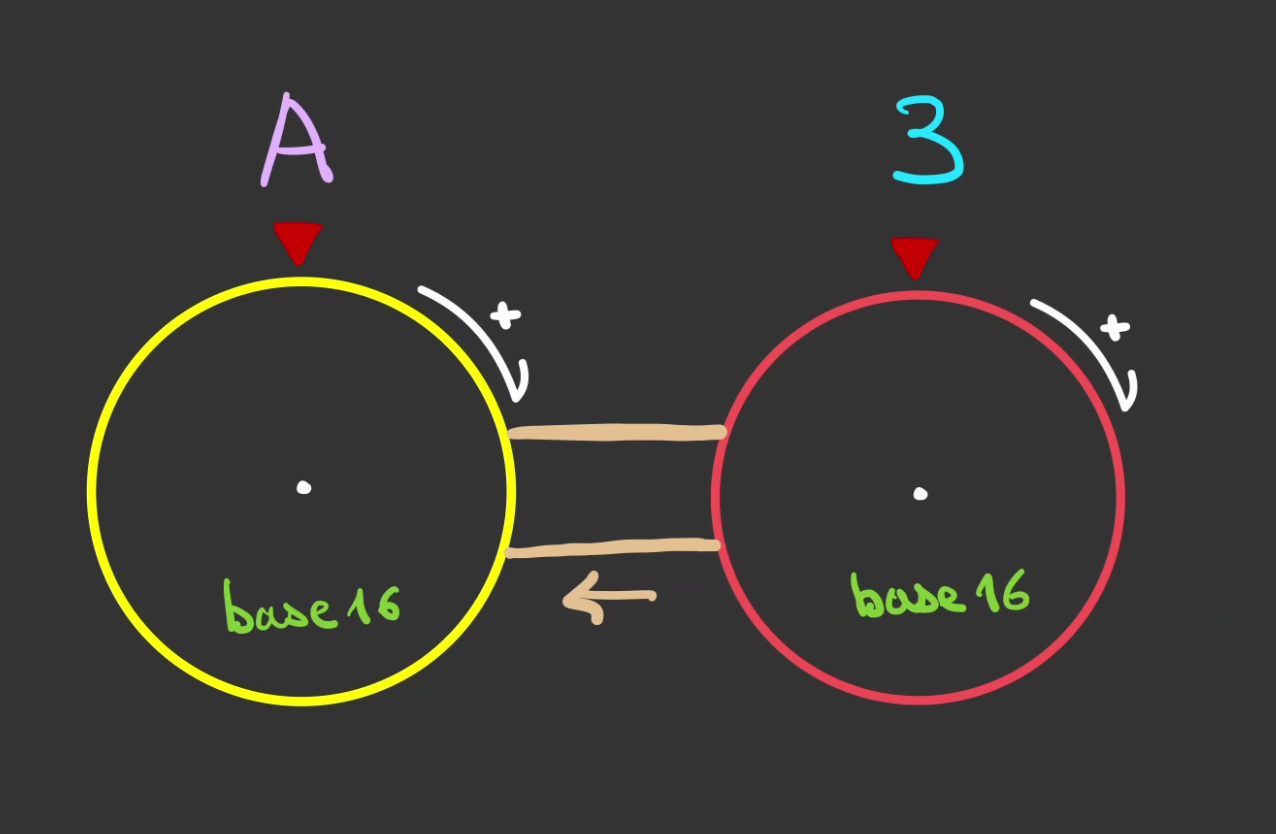
Que l'on décompose en:
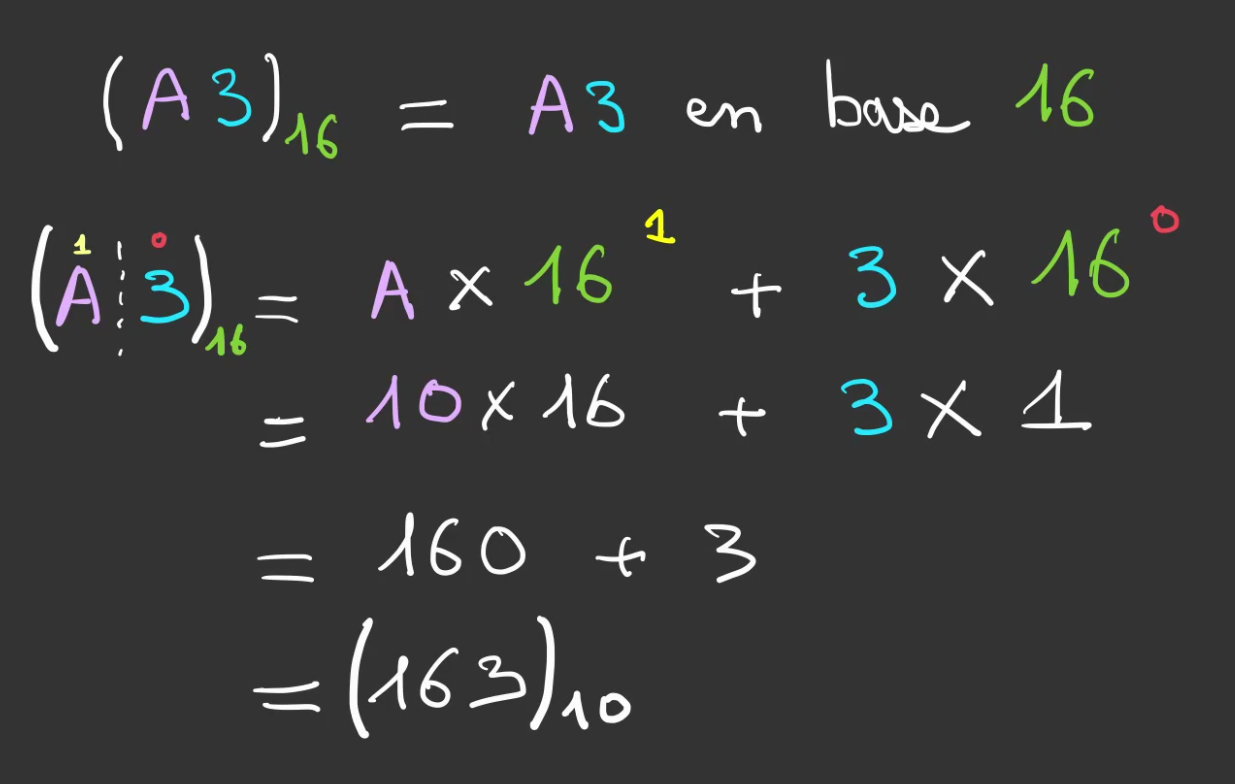
Ce nombre est généralement noté en informatique 0xA3 ou 0xa3.
Nombre à base composite
Vous l'utilisez tous les jours.
Ce sont les secondes, minutes, heures, jours et semaines.
- 60 secondes => 1 minute
- 60 minutes => 1 heure
- 24 heures => 1 journée
- 7 journées => 1 semaines
le saviez-tu
La base 12 provient du nombre de phalanges dans une main. Si on en utilise 2, on arrive à une base 24.
La base 60, est constitué de la base 12 d'une main et des 5 doigts de l'autre main 5*12 = 60.
6 phalanges 3 doigts => 6 + 3*12 = 36 + 3 = 39
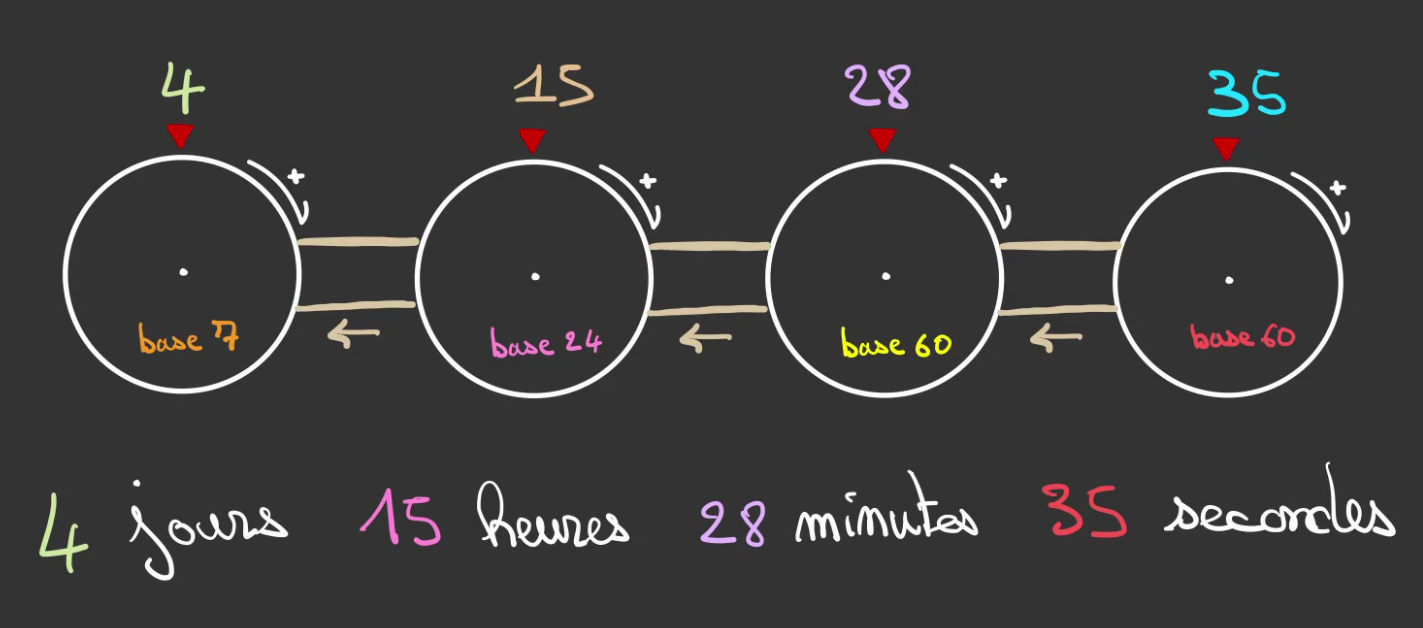
On peut alors procéder à la décomposition.
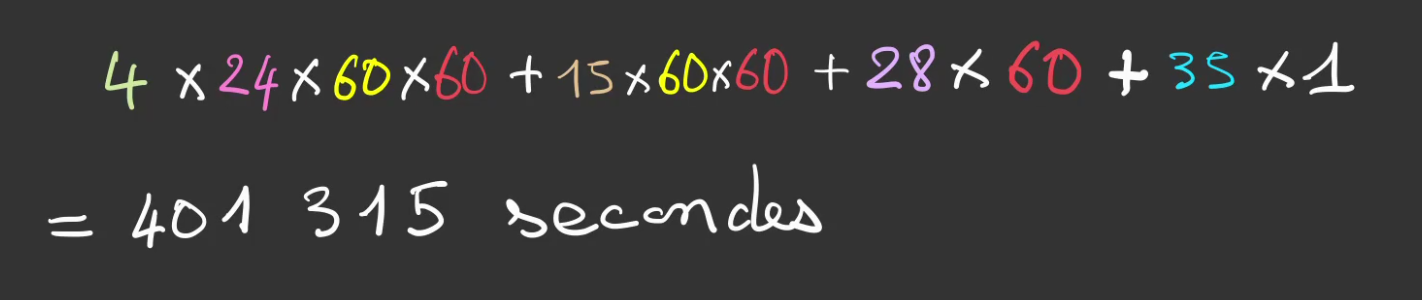
En procédant à la même décomposition lorsque toutes les roues sont en base 2.
L'on peut comprendre pourquoi la notation en puissance de 2 est possible.
Il s'agit d'un cas particulier lorsque les bases sont identiques.
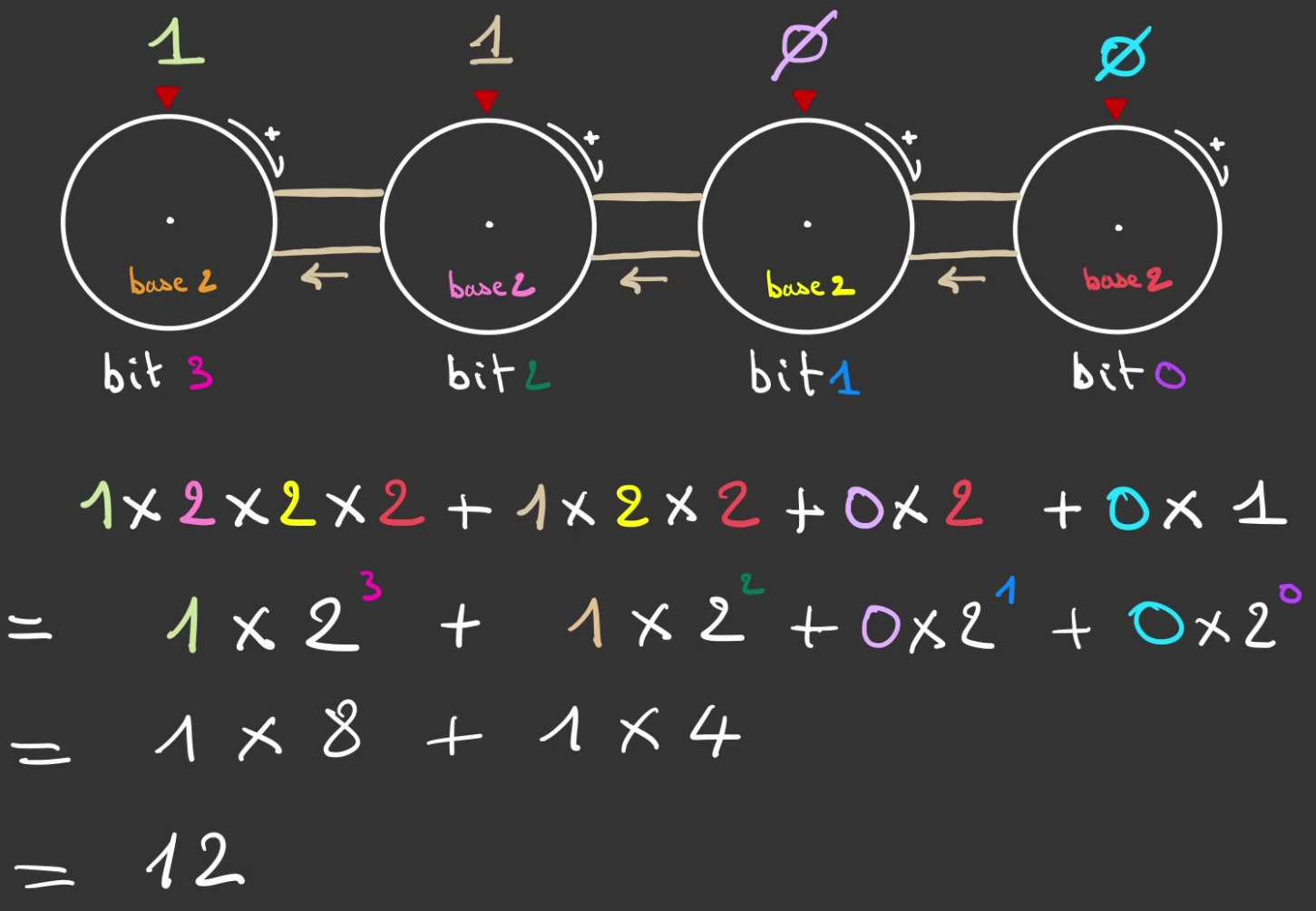
Conclusion
Un même nombre peut avoir une infinité de représentation différentes.
Certaines représentations possèdent des noms:
- représentation décimale :
28 - représentation héxadécimale :
0x1c - représentation binaire :
0b11100
Ces représentation ont pour particularité d'avoir une base constante.
Ce travail est sous licence CC BY-NC-SA 4.0.