Initiation aux shaders (Partie 1)

2020-12-24

la guerre

Bon je vais pas vous mentir j'ai à peu près 3 jours d'expérience sur le sujet, voyez plutôt ça comme une sorte de cahier de route de ma découverte du domaine.

J'ai trouvé deux outils pour faciliter mon initiation:

Le premier est un peu la bible du débutant, le second permet d'expériencer facilement ce que l'on apprend.

En route pour l'aventure 🐱‍👓

Hello world sauce shader

Ce qui déroute en premier lorsque l'on lance shadertoy, c'est l'absence de ce que l'on connait d'habitude.

Le main est déjà très étrange:

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

}

Cela ressemble vaguement à du C mais il y des différences. Le main qui s'applle mainImage prend deux paramètres:

out vec4 fragColor
in vec2 fragCood

Beaucoup de choses déjà dans ces deux paramètres. D'abord les mots-clefs in/out. Ils agissent comme des sas entre le code que l'on écrit et le code qui appelle le code que l'on écrit.

Opérateur de liaison

in défini une variable qui peut-être modifié par notre code sans pouvoir impacter le code appelant, en forçant la recopie de la variable
out défini une variable qui n'est pas initialisée par le code appelant mais qui peut être utilisé par celui-ci à l'issue de l'éxécution de la fonction. C'est dans les faits une référence.

Les vecteurs

Ensuite vient les termes vec4 et vec2, ce sont des structures de données semblables à des tableaux de float (toujours des floats), mais boosté aux stéroïdes. Il existe en effet tout une collection de facilté d'écriture.

Il est par exemple possible de déclarer un vec2 ainsi:

vec2 pos = vec2(1.0, 2.0);

Et accéder à ses composantes de cette manière:

float x = pos.x; // 1.0
float y = pos.y; // 2.0

On peut aussi opérer des inversions de composantes

vec2 inverted_pos = pos.yx; // (2.0, 1.0)

Il est aussi possible de faire de la récupération partielle de composantes

vec3 pos = vec3(1.0, 2.0, 3.0);
vec2 pos2 = pos.xz; // (2.0, 3.0)

Ou même dupliquer des composantes

vec3 pos = vec3(1.0, 2.0, 3.0);
vec3 pos2 = pos.xxx; // (1.0, 1.0, 1.0)

Dernier outil que je connais, il est possible de ne pas complètement définir un vecteur

vec3 pos = vec3(0.0); // (0.0, 0.0, 0.0)
vec3 pos2 = vec3(4.0); // (4.0, 4.0, 4.0)

Les nom de variables du main

Avant de parler de tout ça une petite remise en contexte est nécessaire.

Le mainImage n'est pas vraiment le main du programme. Un shader est une routine qui s'éxécute sur chaque pixels d'une image.

Pour rappel, un pixel est la plus petite unité qui compose une image, pixel ( picture element ).

Afin de rendre une image on ne peut décemment pas traiter un à un les pixels ça serait beaucoup trop long et gourmand en ressources, surtout avec les résolutions d'aujourd'hui qui sont gigantesques comme la 4k et la 8k.

L'idée qui a été choisi est de paralléliser les traitements de chacun des pixels.

Cela implique que le traitement entre deux pixels est totalement indépendant car il doit s'effectuer au même moment.

Un pixel est composé de 3 lampes, une rouge, une bleue et une verte. En fonction de la valeur de chaque composante on est capable de générer n'importe quelle couleur du spectre visible.

Couleur du pixel

Le but de notre routine est de définir l'intensité des lampes rouge, verte et bleue.

Le résultat de notre calcul doit être affecté dans la variable fragColor. Celle-la est un vec4, cela signifie qu'elle possède 4 composantes: (Rouge, Vert, Bleu, ?).

La dernière est le canal alpha qui gère la transparence. On ne s'en occupera pas dans cette partie.

Dernière chose à savoir est que chacune de ces composantes se répartissent entre 0 ( pas de lumière du tout ) et 1 ( intensité maximale ).

Le code ci-dessous explique de renvoyer pour chaque pixel de l'image un vecteur (1.0, 0.0, 0.0, 1.0) autrement dit du rouge pur. La 4ème composante est à 1.0 pour signifier qu'il n'y a pas de transparence.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Output to screen
    fragColor = vec4(1.0, 0.0, 0.0, 1.0);
}

Mais aussi du vert

fragColor = vec4(0.0, 1.0, 0.0, 1.0);

Mais aussi du bleu

fragColor = vec4(0.0, 0.0, 1.0, 1.0);

Mais aussi du jaune

fragColor = vec4(1.0, 1.0, 0.0, 1.0);

Bref vous voyez l'idée. Notre routine contrôle chaque pixel de l'écran qui mis tous ensemble forme l'image finale.

La position du pixel

Bon tout ça c'est très bien mais un peu limité tous les pixels ont la même couleur on est pas près de faire le nouveau Pixar à la mode. 😋

C'est là qu'intervient notre second paramètre fragCoord il s'agit là aussi d'un vec2, la première composante est l'abscisse du pixel sur l'écran et la deuxième son ordonnée dans la pratique (x, y).

Essayons de visualiser cela 🧐

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    // Output to screen
    fragColor = vec4(fragCoord.x, 0.0, 0.0 ,1.0);
}

Rouge, encore! Mais c'est normal quand on y réfléchi, les coordonnées des pixels sont données sous leur forme cartésiennes, c'est à dire des nombres entiers positifs.

Or les composantes de couleur ne peuvent pas dépasser la valeur 1.0.

Il va donc falloir normaliser les valeurs. Pour cela on va utiliser un autre outils mis à disposition par le langage de shader qui nous fourni tout une série de variable appelée des uniforms.

Il faut les voir comme le moyens de communiquer des informations entre les différentes unité de traitement de pixels. Celle qui va nous intéresser ici est iResolution. Elle contient la taille en pixels de l'écran et donc le nombre en X et en Y de pixels.

Ce qui va nous permettre d'effectuer une règle de trois entre la position du pixel et la résolution.

iResolution.x       -> rouge pur (1.0)
fragCoord.x         -> intensité de rouge  (X)

X = (fragCoord.x * 1.0) / iResolution.x

En utilisant les propriétés des vecteurs:

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = fragCoord / iResolution.xy;

    // Output to screen
    fragColor = vec4(uv.x, 0.0, 0.0 ,1.0);
}

De même en Y

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = fragCoord / iResolution.xy;

    // Output to screen
    fragColor = vec4(uv.y, 0.0, 0.0 ,1.0);
}

On peut même cartographier les deux composantes

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = fragCoord / iResolution.xy;

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
}

Le noir est une absence de luminosité autrement dit (0.0, 0.0, 0.0, 1.0).

Le jaune une combinaison de rouge et de vert, le jaune pur représente (1.0, 1.0, 0.0, 1.0).

En prenant la formule à l'envers on peut déterminer l'origine du repère de notre écran ainsi que le sens du repère.

Pour une résolution de 800x450, il vient:

Changement de repère

Bon je sais pas vous mais le repère en bas à gauche n'a jamais été ma tasse de thé ou de café pour les amateurs.

Je préfère que l'origine de mon repère soit le centre de mon écran, cela va faciliter grandement les calculs qui vont suivre. (oui il va y avoir un max de maths 🤓).

Pour mettre le centre au centre on va retrancher la moitié de la résolution sur chacune des composantes.

Cette soustraction va automatiquement nous amener à obtenir des valeurs négatives. Une composante de couleur étant toujours positive, une valeur négative sera mise à 0.0.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = fragCoord - 0.5 * iResolution.xy;

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
}

On se retrouve avec 4 quadrants:

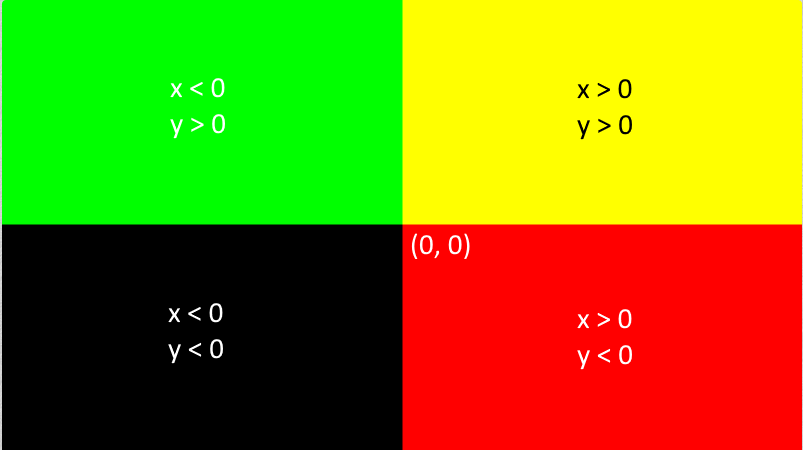
Que l'on peut avec la même technique que tout à l'heure visualiser de manière plus précise sous la forme d'un continuum.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = (fragCoord - 0.5 * iResolution.xy) / (iResolution.xy / 2.0);

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
}

Dessiner des formes simples

Le disque

C'est la forme la plus simple à afficher.

Son équation dans le plan cartésien est :

x² + y² < R²

Comme on a centré le repère, il n'y a pas besoin de se soucier d'offset.

en prenant la racine de chaque côté

sqrt(x² + y²) < R

Le langage fourni une fonction appellée length qui permet de récupérer la norme d'un vecteur.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = (fragCoord - 0.5 * iResolution.xy) / (iResolution.xy / 2.0);

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
    
    if (length(uv) < 1.0) {
        fragColor = vec4(1.0, 1.0, 1.0 ,1.0);
    }
}

Bon c'est presque ça, on a juste négligé le ratio de notre image. Pour rétablir le disque on peut diviser nos coordonnées par la résolution en Y sur 2.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = (fragCoord - 0.5 * iResolution.xy) / (iResolution.y / 2.0);

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
    
    if (length(uv) < 1.0) {
        fragColor = vec4(1.0, 1.0, 1.0 ,1.0);
    }
}

Et tada 🎉 un disque!

Un triangle équilatéral

Je vais pas vous mentir, ça n'a pas été très facile de déterminer comment dessiner le triangle.

Le principe reste le même: déterminer si un point appartient ou non à une surface.

Le problème ici est que la forme est bien plus complexe qu'un disque.

Il faut donc ruser pour trouver une solution

Une petite simulation avec geogebra m'a permis de me simplifier la représentation du problème.

Si M est en dehors de l'angle AB, AC. La valeur de d est négative.

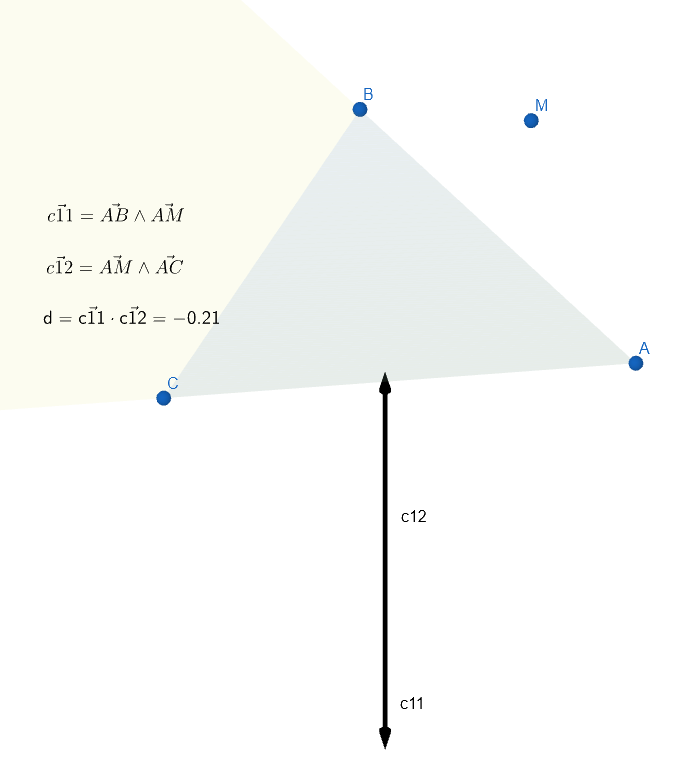
De même dans l'autre sens

Par contre si l'on se trouve dans l'angle, la valeur d devient positive.

Le problème c'est que si le point est dans l'angle mais en dehors du triangle, la valeur reste positive.

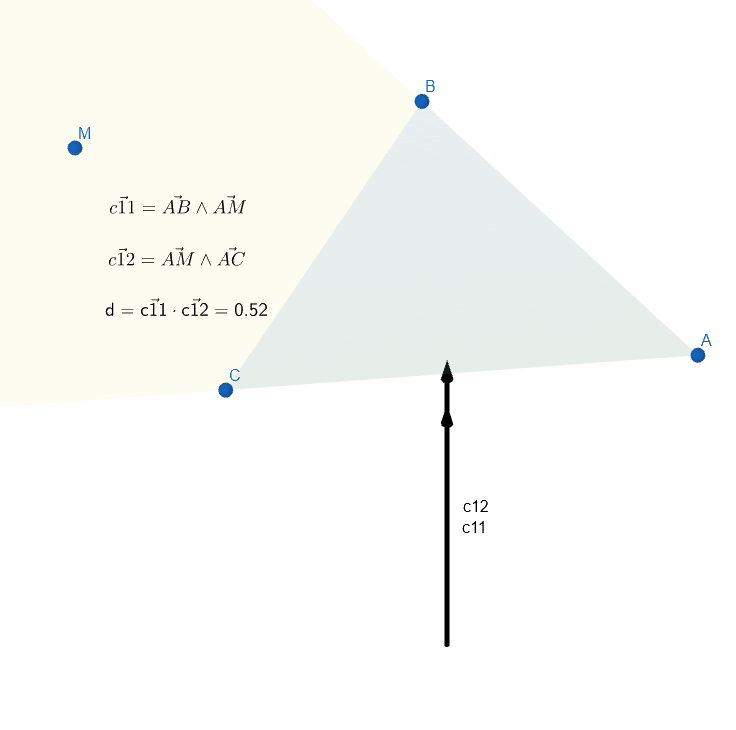
L'idée est d'appliquer l'algorithme sur les 3 angles, pour que le point soit bel et bien à l'intérieur du triangle. Si chacun des produits scalaires sont positifs alors le point M appartient au triangle.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{

    vec2 uv = (fragCoord - 0.5 * iResolution.xy) / (iResolution.y / 2.0);

    // Output to screen
    fragColor = vec4(uv.x, uv.y, 0.0 ,1.0);
    
    // Coordonnées des sommets du triangles équilatéral
    float k = 1.75;
    vec3 A = vec3(0.0, 0.57, 0.0) * k;
    vec3 B = vec3(0.5, -0.28, 0.0) * k;
    vec3 C = vec3(-0.5, -0.28, 0.0) * k;
    
    // Calcul des coordonnées des vecteurs
    vec3 AB = B-A;
    vec3 AC = C-A;
    
    vec3 BA = A-B;
    vec3 BC = C-B;
    
    vec3 CA = A-C;
    vec3 CB = B-C;
    
    // M est le point que l'on cherche à déterminer s'il est en dehors ou non du triangle
    vec3 AM = vec3(uv - A.xy, 0);
    vec3 BM = vec3(uv - B.xy, 0);
    vec3 CM = vec3(uv - C.xy, 0);
    
    // Calcul des déterminants
    float d1 = dot(cross(AB, AM), cross(AM, AC));
    float d2 = dot(cross(BA, BM), cross(BM, BC));
    float d3 = dot(cross(CA, CM), cross(CM, CB));
    
    // Dessin du cercle de rayon 1
    if (length(uv) < 1.0) {
    
        fragColor = vec4(0.0, 0.0, 1.0 ,1.0);
    }
    
    // Si tous les déterminants sont positifs, le point est dans le triangle
    if (d1 >= 0.0 && d2 >= 0.0 && d3 >= 0.0) {
    
        fragColor = vec4(1.0, 1.0, 1.0 ,1.0);
    }
}

Et un triangle pour la table 12 ! Un ! 👨‍🍳

Champ de Distance Signé

Les deux algorithmes (pour le disque et pour le triangle) sont appelées des SDF : Signed Distance Field ou Champ de Distance Signé.

Un champ est une propriété qui recouvre tout un espace ( ici 2D ). Cela signifie que notre propiété va s'appliquer sur chaque pixel de l'écran.

La deuxième partie est cette idée de distance. On recheche pour tout point de l'écran si l'on est à l'intérieur ou l'extérieur d'une surface donnée et surtout à quelle distance on se trouve d'elle.

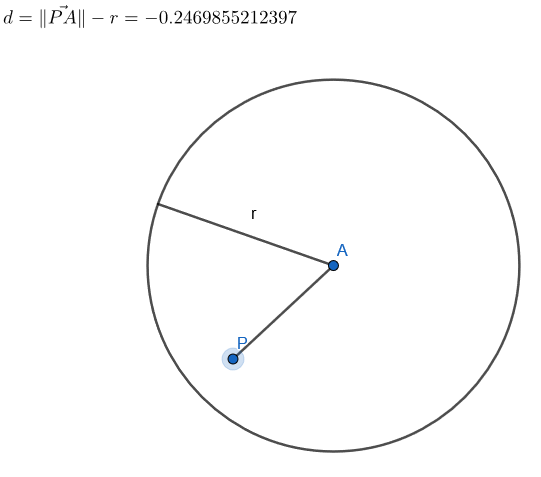
Reprenons le disque qui est un peu plus simple. Son champ de distance est donné en tout point de l'écran par la relation suivante:

Distance du point observé par rapport au centre du disque - rayon du disque

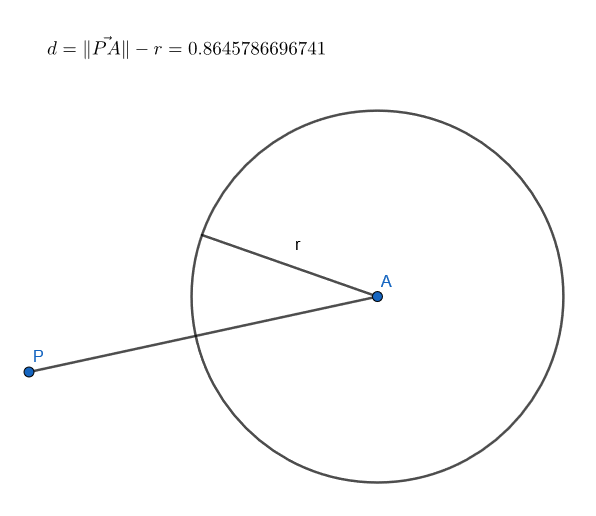
Tout ce que l'on fera par la suite sera de calculer la SDF de nos forme.

Et pourquoi "signé", parce que si l'on est à l'intérieur de la du disque, la distance devient négative.

Conclusion

C'est tout pour aujourd'hui!

La suite sera de se plonger dans le monde merveilleux de la 3D enfin de la projection de la 3D sur un écran 2D.

On y verra notamment le RayMarcher.

Bonne Fêtes à toutes et tous et merci de m'avoir lu. 🤗

Auteur: Akanoa

Je découvre, j'apprends, je comprends et j'explique ce que j'ai compris dans ce blog.

Ce travail est sous licence CC BY-NC-SA 4.0.