Initiation aux shaders : RayMarching (Partie 2)

On a vu dans la partie précédente comment manipuler les pixels d'une image grâce au langage de shader.

Il est temps de s'attaquer à du bien plus intéressant: la 3D ! 😎

L'algorithme de RayMarching

Littéralement "marché de rayon".

L'idée est très élégante. Elle se base entièrement sur le principe des SDF (Signed Distance Field).

On a comme situation de départ un oeil situé au centre de l'écran mais reculé d'une certaine distance.

La situation est représentée vu de haut.

On veut afficher notre objet en bleu.

On choisi un pixel sur notre écran.

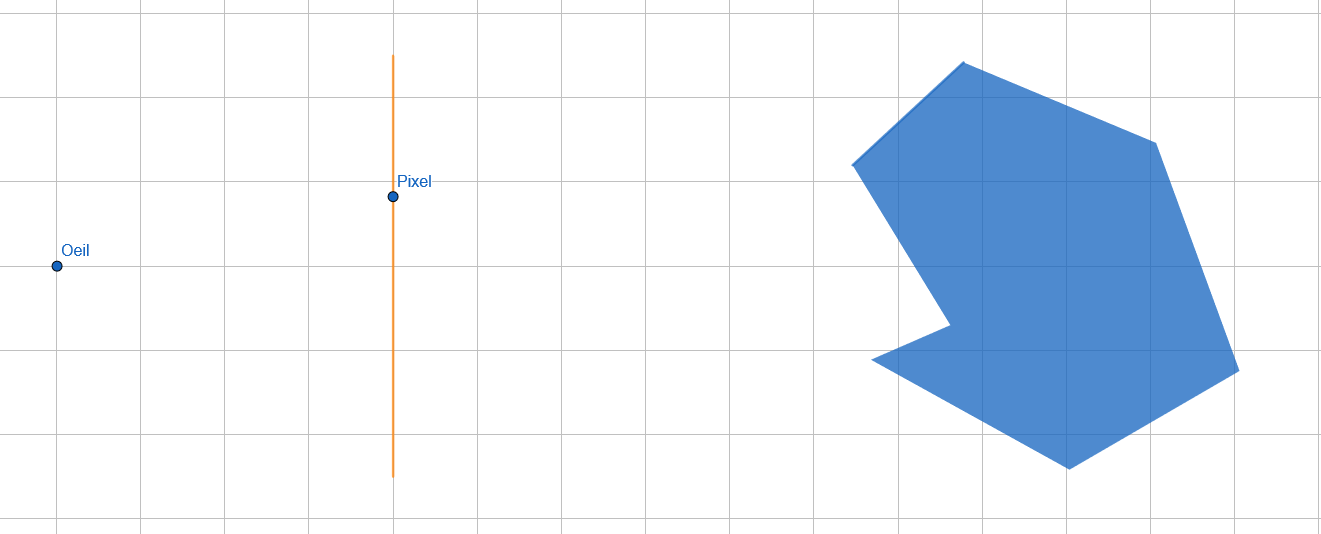
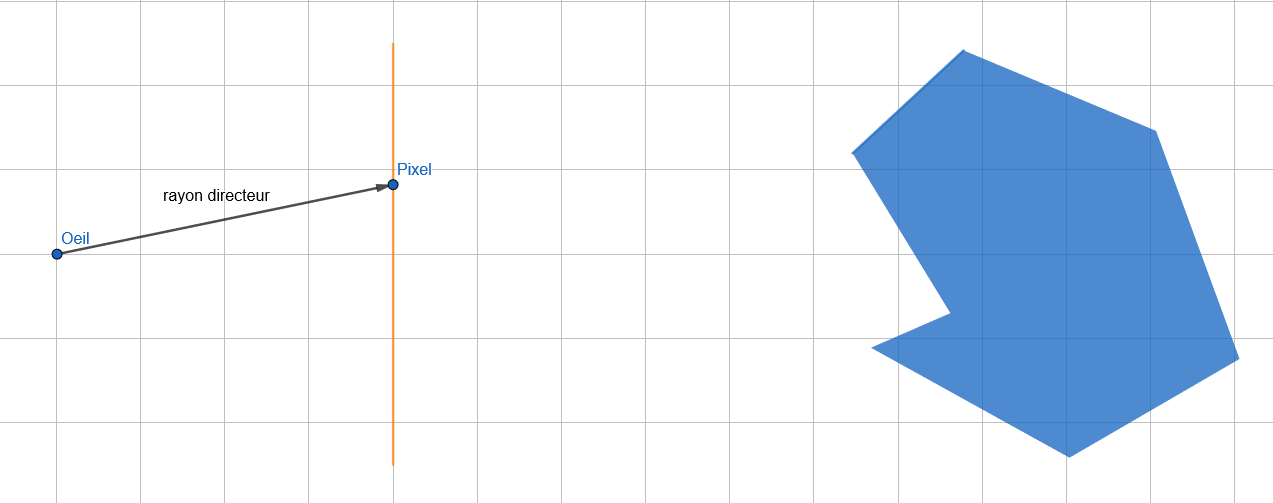
On détermine un rayon directeur entre notre oeil et le pixel.

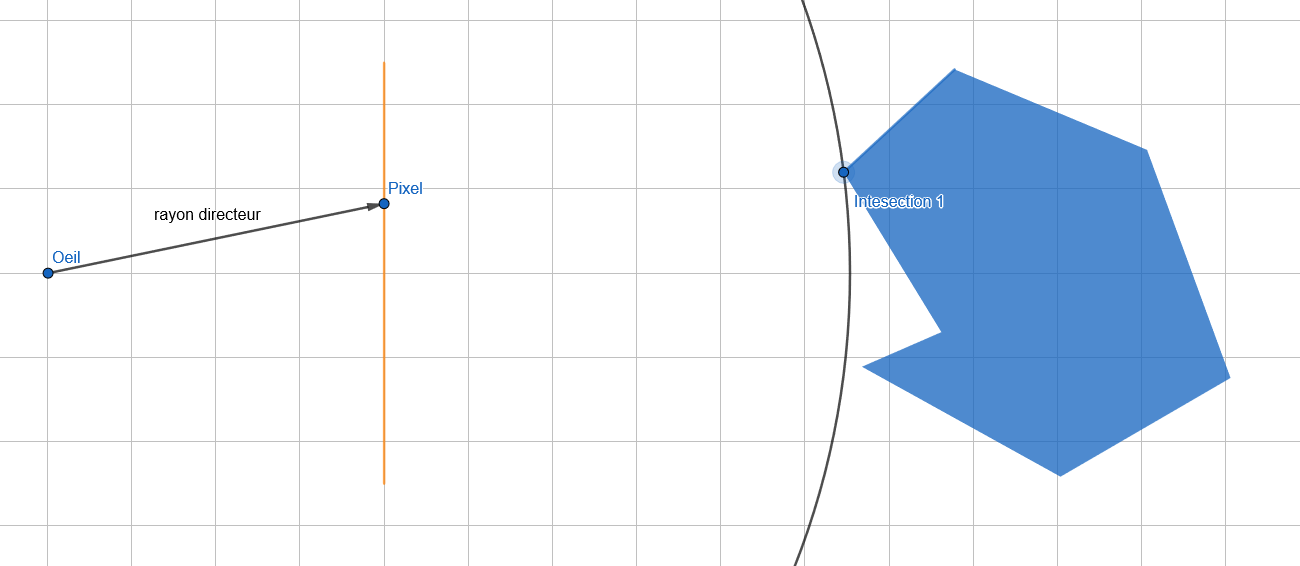
Grâce à la SDF de notre solide on détermine la distance de l'objet par rapport à notre oeil et on trace un cercle du rayon de la distance nous séparant de l'objet. Autrement dit le point du solide le plus proche de l'oeil.

Puis on trace un rayon infini partant de l'oeil et dans la direction du vecteur. Le point d'intersection M entre le cercle que l'on vient de tracer devient notre nouveau point de départ.

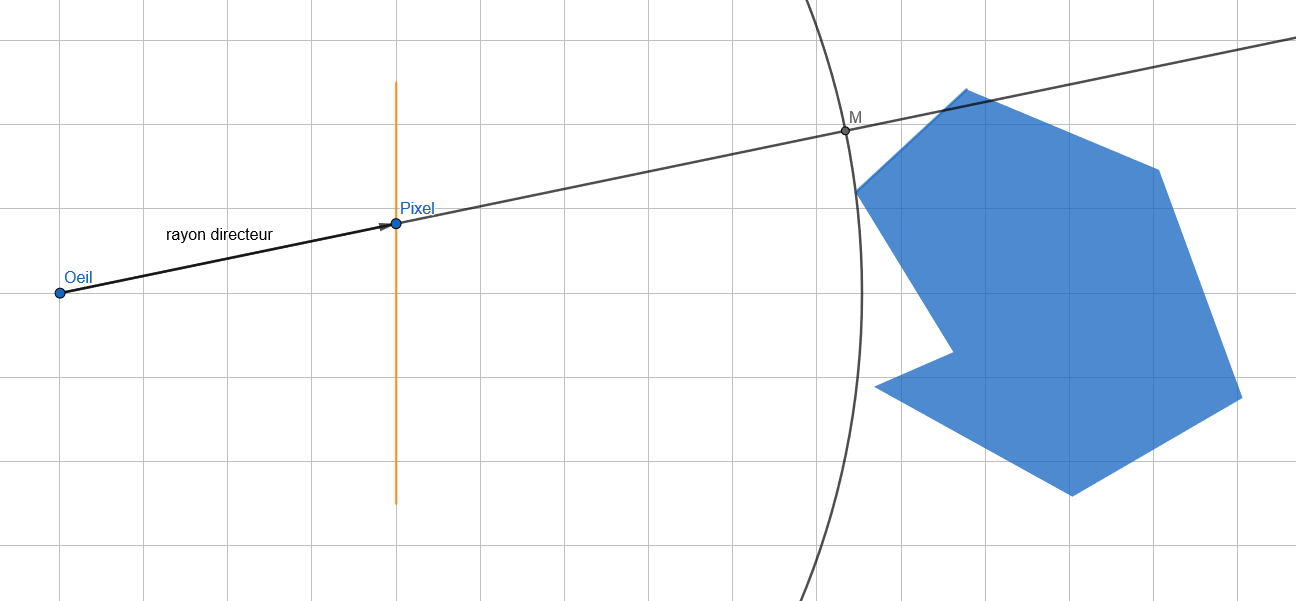
On réitère l'opération de ce point M comme oeil.

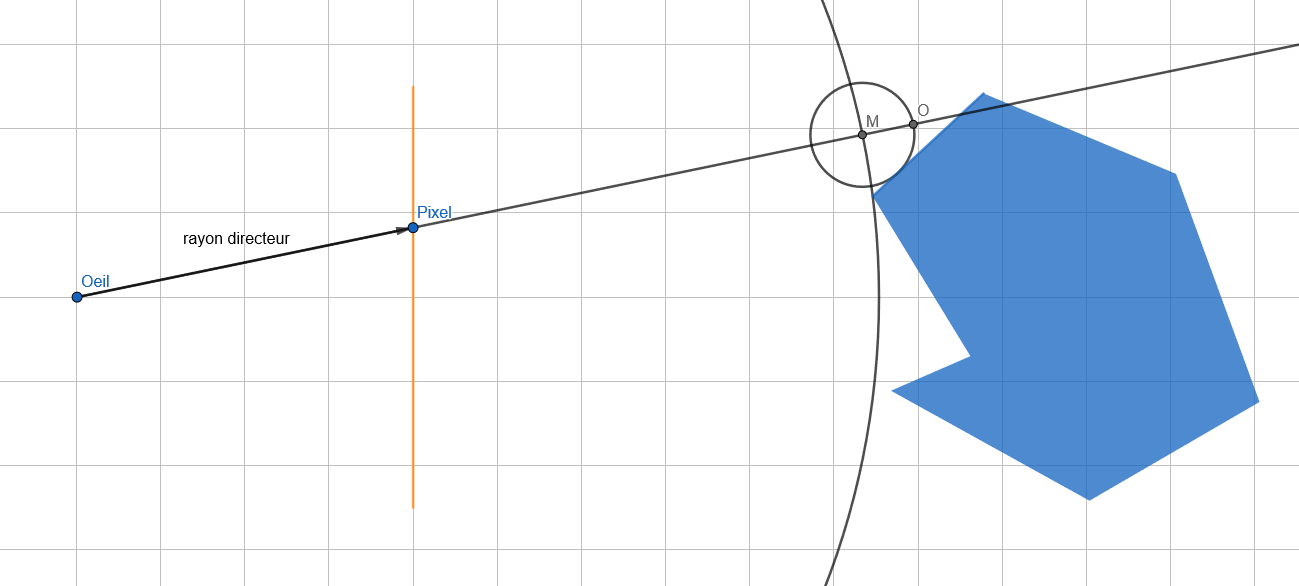
On récupère un point O et rebelote.

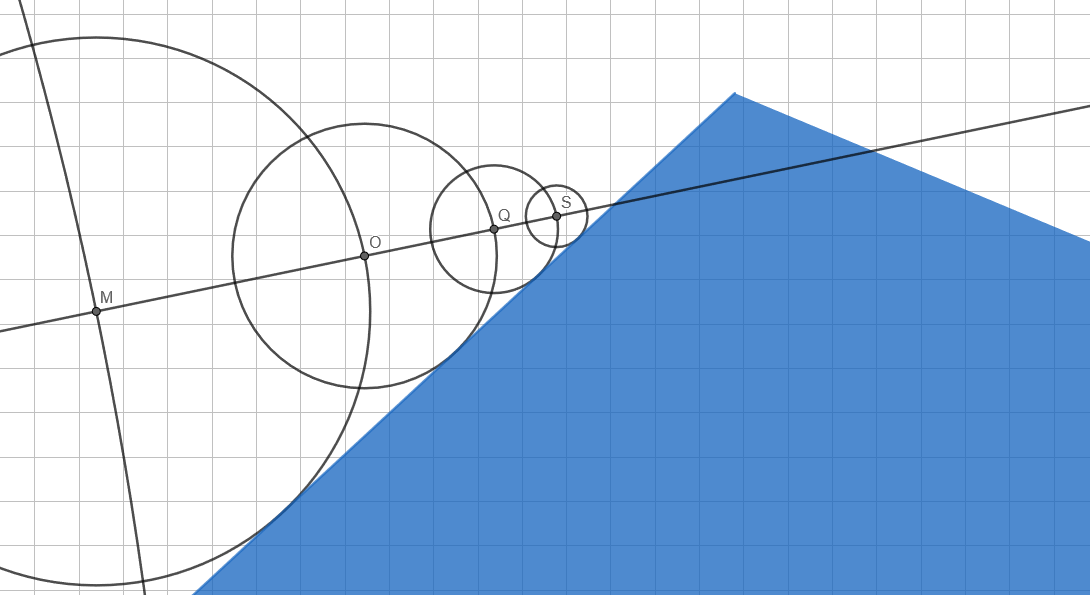
Lorsque le diamètre du cercle obtenu est suffisamment petit, on considère que l'on a touché l'objet.

On somme l'ensemble des distances trouvées précédemment et l'on retourne la somme.

Il existe le cas ou le rayon ne touche pas l'objet alors le diamètre du cercle va être trop grand.

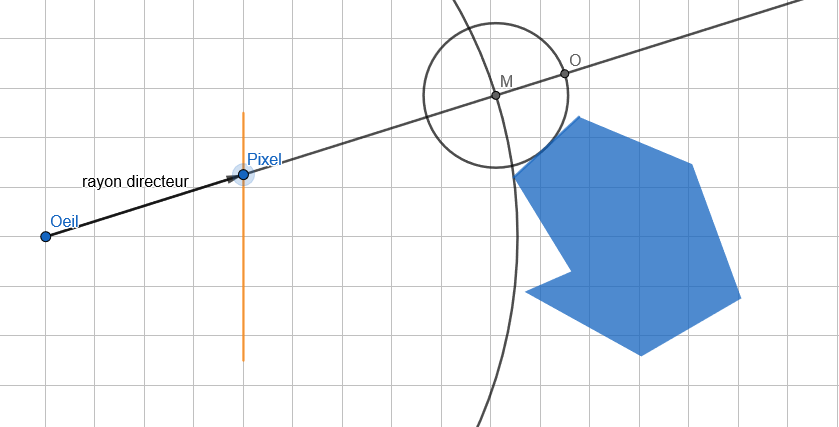
Si la distance est trop grande on la renvoie la distance maximale.

Ce qui est important de comprendre c'est que l'on va efectué cette algorithme un très grand nombre de fois et plusieurs fois par frame. Autant optimiser tout ce qui peut l'être. 😉

Implémentation

Pour nous faciliter la vie on va définir quelques constantes:

#define MIN_DISTANCE 0.001
#define MAX_DISTANCE 20.
#define MAX_ITERATIONS 50

Pui on implémente l'algorithme de raymarching en lui-même.

float rayMarch(vec3 rayOrigin, vec3 rayDirector) {
    
    // Initialisation des distances
    float accumulatedDistance = 0.0;
    float computedDistance = 0.0;
    vec3 currentPoint;
    
    // Boucle de l'algorithme d'au plus MAX_ITERATIONS
    for(int i = 0; i < MAX_ITERATIONS; i++) {
    
        // Calcul du point courant
        currentPoint = rayOrigin + rayDirector * accumulatedDistance;
        
        // Calcul de la distance du point courant par rapport à une sphère
        // de rayon 0.5 et décalé de 0.5 vers la droite et avancé de 1.8 de l'écran
        computedDistance = length(currentPoint - vec(0.5, 0, 1.8)) - 0.5;
        
        // On accumule la distance trouvée
        accumulatedDistance += computedDistance;
        
        // Si la distance trouvé est suffisamment faible on stoppe l'algorithme
        if ( computedDistance < MIN_DISTANCE ) {
            break;
        }
        
        // Si la distance trouvée est trop grange on retourne la distance
        if( accumulatedDistance > MAX_DISTANCE ) {
            return MAX_DISTANCE;
        }
    
    }
    
    return accumulatedDistance;
}

Puis on calcule les paramètres de notre algorithme

    // Calcule des UV de l'écran
    vec2 uv = (fragCoord- 0.5*iResolution.xy) / iResolution.y;
    
    // La caméra est au centre du monde
    vec3 eye = vec3(0);
    
    // L'écran est décalé de 1
    vec3 pixel = vec3(uv, 1.0);
    
    // Calcul du rayon directeur de l'oeil traversant le pixel
    vec3 rayDirector = normalize(pixel - eye);

Le rayon directeur doit-être unitaire. D'où l'utilisation de la méthode normalize.

Pour rappel les UVs sont des coordonnées dont l'origine est au centre de l'écran et dont les coordonnées sont transformé pour que l'axe des Y dans un ratio 16:9 soit situés entre [-1, 1].

On applique en suite l'algorithme de raymarching avec les paramètres calculés.

    // On applique l'algorithme de raymarching à ce pixel
    float d = rayMarch(eye, rayDirector);

On désire afficher cette distance sous la forme d'une composante de couleur. On doit donc compresser les distances pour les faire rentrer dans l'intervalle [0, 1].

Et on affiche sous forme de niveau de gris notre sphere.

    // On tasse les distances pour les faire rentrer dans l'intervalles [0, 1]
    d /= MAX_DISTANCE;

    // On affiche
    fragColor = vec4(d, d, d, 1.0);

Et cette fois-ci on affiche une sphère et non pas un disque! Bienvenu dans la 3ème dimension !! 😎

Pour s'en convaincre on peut booster le contraste et la luminosité de l'image.

On remarque des cercles concentriques décalés vers la gauche. Plus le disque est sombre plus il est proche d'une distance de 0.

On est bien en face d'un objet dans la 3ème dimension.

Plusieurs objets dans notre scène

Notre monde est un peu vide, il est temps de le remplir.

Dessiner un plan horizontal

Un plan horizontal est défini par l'ensemble des points qui sont à la même hauteur.

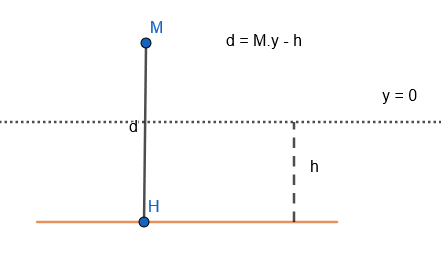
On défini la SDF du plan

float horizontalPlan(float height, vec3 point) {
    return point.y - height;
}

Elle prend en paramètre la hauteur du plan par rapport au plan XZ de notre monde. Ainsi que le point dont on cherche la distance par rapport au plan.

Pour tester notre code on va opérer une petite modification.

On va définir la SDF de ce plan.

float horizontalPlan(float height, vec3 point) {
    return point.y - height;
}

Puis une fonction scene qui prend en compte le point dont lequel on désire connaître la distance par rapport à la scène.

float scene(vec3 point) {    
    // Un plan 0.2 unité plus bas que le plan XZ
    return horizontalPlan(-.2, point);
}

On va par la même occassion se définir une SDF pour la sphère.

float sphere(vec3 center, vec3 point, float rayon) {
    return length(point - center) - rayon;
}

Et on modifie la fonction de raymarching

float rayMarch(vec3 rayOrigin, vec3 rayDirector) {
    
    // Initialisation des distances
    float accumulatedDistance = 0.0;
    float computedDistance = 0.0;
    vec3 currentPoint;
    
    // Boucle de l'algorithme
    for(int i = 0; i < MAX_ITERATIONS; i++) {
    
        // Calcul du point courant
        currentPoint = rayOrigin + rayDirector * accumulatedDistance;
        
        // Calcule de la distance du point courant par rapport à la scene
        computedDistance = scene(currentPoint);
        
        // On accumule la distance trouvée
        accumulatedDistance += computedDistance;
        
        // Si la distance trouvé est suffisamment faible on stoppe l'algorithme
        if ( computedDistance < MIN_DISTANCE ) {
            break;
        }
        
        // Si la distance trouvée est trop grange on retourne la distance
        if( accumulatedDistance > MAX_DISTANCE ) {
            return MAX_DISTANCE;
        }
    
    }
    
    return accumulatedDistance;
}

Ce qui nous permet d'afficher ceci 😃

On obtient bien ce qui est attendu. la ligne d'horizon tend bien vers le plan car elle se trouve à une distance trop importante.

Afficher plus d'un élément.

Pour afficher plus d'un élément il faut se représenter les choses ainsi

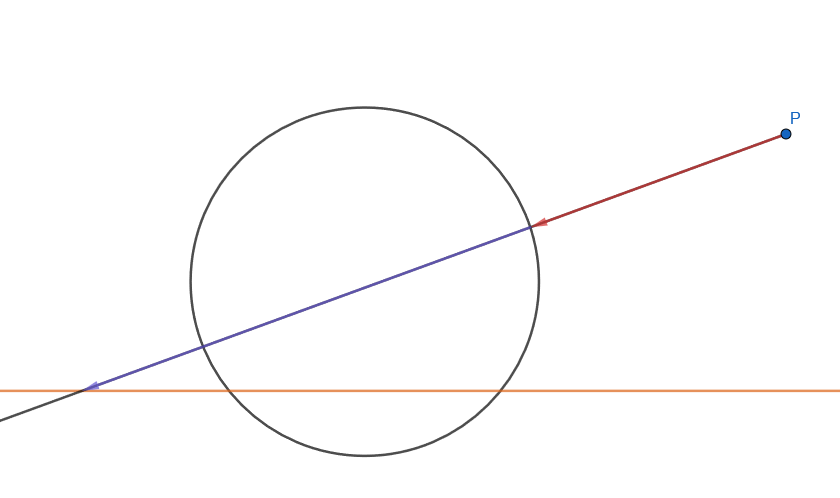
Partant du point P et suivant ce rayon précis la sphère est plus proche de P que le plan (orange).

Autrement dit la SDF de la sphère va renvoyer une distance plus faible que le plan.

Mathématiquement ce concept peut-être représenté par le minimum des deux distances.

float scene(vec3 point) {
    
    float dSphere = sphere(vec3(0.5, 0, 2.), point, .7);
    float dPlan = horizontalPlan(-.2, point);
    
    return min(dSphere, dPlan);
}

Ce qui nous permet d'afficher les deux éléments.

Mais il manque quelque chose...

De la couleur ! 🤡

Conclusion

On a appris à afficher très sommairement des solides dans un environnement 3D. Et sans bibliothèques complexes.

La prochaine fois on rajoutera de la couleur, des ombres et de la lumière!

Je vous donne aussi le lien de mon shadertoy.

Je vous remercie de m'avoir lu 😀.

Auteur: Akanoa

Je découvre, j'apprends, je comprends et j'explique ce que j'ai compris dans ce blog.

Ce travail est sous licence CC BY-NC-SA 4.0.