Initiation aux shaders : Matériel, Ombres et Lumière (Partie 3)

2021-01-29

Lors de la précédente partie nous étions laissés avec un résultat sympa mais qui ne casse pas 3 pattes à un canard!

Comme promis dans sa conclusion nous allons nous attaquer à rajouter de la couleur dans tout ça. 🌈

Le Matériel

Afin d'appliquer un matériel sur un objet de notre scène on va devoir expliquer au raymarcher ce qu'il doit faire lorsqu'il touche un objet et de quelle couleur le pixel de l'écran associé doit être coloré.

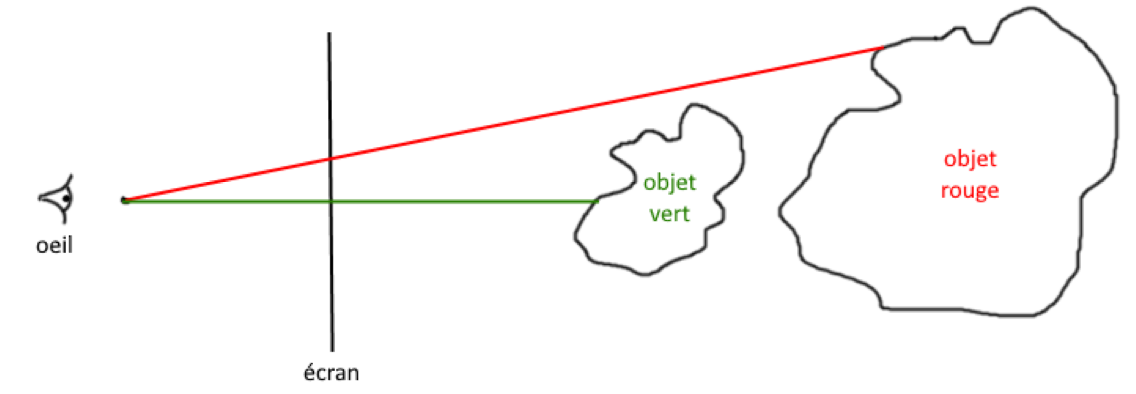
Un rayon part de l'oeil traverse l'écran et continue sa course jusqu'à rencontrer un objet de notre scène. Si le rayon touche l'objet vert, le pixel traversé par le rayon doit être coloré en vert. Et à l'inverse si c'est l'objet rouge qui est touché, le pixel doit devenir rouge.

Pour cela il nous faut un moyen de stocker l'information de couleur en fonction de l'objet touché.

On va donc opérer à quelques modification de notre modèle de données.

Tout d'abord on créé une structure qui va nous permettre de stocker à la fois la distance de l'objet par rapport à l'oeil, ainsi que son information de couleur.

Pour ne pas stocker des données trop lourdes on va uniquement définir un entier qui sera l'index de notre matériel à appliquer au solide s'il est touché par un rayon venant de l'oeil.

Modifications du code existant

Implémentation de la structure de données

struct Data {
    float d; // distance signée entre l'objet touché et l'oeil
    int m;   // index du matériel à appliquer
}

On va devoir faire aussi faire quelques modifications et ajouts:

Tout d'abord, on doit définir quelques fonctions permettant de manipuler notre structure.

Notamment une fonction de minimum entre deux struct Data

/**
* Retourne le minimum entre deux structures de données en se basant sur la distance signée.
* d1 : structure 1
* d2 : structure 2
*/
Data minData(Data d1, Data d2) {
    
    if(d1.d < d2.d) {
        return d1;
    }
    return d2; 
}

Modification des SDF existantes

On doit aussi modifier nos deux fonctions SDF (Signed Distance Field) pour le plan et la sphère.

SDF de la sphère

/**
* Retourne la distance signée d'une sphère par rapport à l'oeil
* point: Point de la scène 3D touché par le rayon de lumière
* rayon: Rayon de la sphère
*/
float sdSphere(vec3 point, float rayon) {
    return length(point) - rayon;
}

devient

/**
* Retourne la distance signée d'une sphère par rapport à l'oeil
* point    : Point de la scène 3D touché par le rayon de lumière
* radius   : Rayon de la sphère
* material : Matériel à appliquer à la sphère 
*/
Data sdSphere(vec3 point, float radius, int material) {
    return Data(length(point) - radius, material);
}

SDF de la plan

/**
* Retourne la distance signée d'un plan horizontal par rapport à l'oeil
* point    : Point de la scène 3D touché par le rayon de lumière
* height   : Rayon de la sphère
*/
float sdHorizontalPlan(vec3 point, float height) {
    return point.y - height;
}

Devient

/**
* Retourne la distance signée d'un plan horizontal par rapport à l'oeil
* point    : Point de la scène 3D touché par le rayon de lumière
* height   : Rayon de la sphère
* material : Matériel à appliquer au plan
*/
Data sdHorizontalPlan(vec3 point, float height, int material) {
    return Data(point.y - height, material);
}

Modification de la fonction de génération de scène

/**
* Renvoie la distance signée de l'intégralité des objets de la scène
* point : Point de la scène qui doit être calculé
*/
float scene(vec3 point) {
    
    float dSphere = sphere(point - vec3(0.5, 0, 2.), .7);
    float dPlan = sdHorizontalPlan(point, -.2);
    
    return min(dSphere, dPlan);
}

devient

/**
* Renvoie la distance signée et le matériel associé de l'intégralité des objets de la scène
* point : Point de la scène qui doit être calculé
*/
Data scene(vec3 point) {
    
    Data dSphere = sdSphere(point - vec3(0.5, 0, 2.), .7, MATERIAL_RED);
    Data dPlan = sdHorizontalPlan(point, -.2, MATERIAL_GREEN);
    
    return minData(dSphere, dPlan); // le minimum de distance entre les deux structures
}

Modification de l'algorithme de raymarching

On doit aussi modifier la fonction de Raymarching

Il devient:

/**
* Calcule la distance de l'objet le plus proche par rapport à l'oeil 
* en fonction d'un rayon directeur
* rO : origine du rayon
* rD : vecteur directeur du rayon
*/
Data rayMarch(vec3 rO, vec3 rD) {
    
    float d = 0.0;
    int m = 0;
    for(int i=0; i < MAX_ITERATIONS; i++) {
        
        vec3 p =  rO + rD * d;
        Data ds =  scene(p);
        d += ds.d;
        m = ds.m;
        if (ds.d < MIN_DISTANCE || d > MAX_DISTANCE) break;
    }
    
    return Data(d, m);

}

Dictionnaire de matériel

On définit des constantes qui vont correspondre à

#define MATERIAL_RED   1  
#define MATERIAL_BLUE  2
#define MATERIAL_GREEN 3
#define MATERIAL_YELLOW 4

Puis une fonction qui va associer notre index à une couleur sous forme de vec3.

/**
* Renvoie le matériel associé à l'index ou du noir si l'index est inconnu
* m : index du matériel
*/
vec3 material(int index) {
    switch(index) {
        case MATERIAL_RED:
            return vec3(1.0, 0, 0);
        case MATERIAL_GREEN:
            return vec3(0, 1.0, 0);
        case MATERIAL_BLUE:
            return vec3(0, 0, 1.0);
        case MATERIAL_YELLOW:
            return vec3(1.0, 1.0, 0);
        default:
            return vec3(0);
    }
        
}

Fonction principale

/**
* Calcule la couleur que doit posséder un pixel en fonction de ses coordonnées absolues
* fragColor : Couleur du pixel à afficher à l'écran
* fragCoord : Coordonnées du pixel à l'écran
*/
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Calcule des UV de l'écran
    vec2 uv = (fragCoord- 0.5*iResolution.xy) / iResolution.y;
    
    // La caméra est au centre du monde
    vec3 eye = vec3(0);
    
    // L'écran est décalé de 1
    vec3 pixel = vec3(uv, 1.0);
    
    // Calcul du rayon directeur de l'oeil traversant le pixel
    vec3 rayDirector = normalize(pixel - eye);
    
    // On applique l'algorithme de raymarching à ce pixel
    Data data = rayMarch(eye, rayDirector);

    // On récupère le matériel
    vec3 col = material(data.m);

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui nous donne un très joli levé de soleil dans la plaine 😁

Si vous voulez vous amuser avec voici le code.

Le ciel les oiseaux et ta mère!

Comme vous pouvez le remarquer ( ou justement pas le remarquer 😋 ) notre sol à disparu !

Cela est du au fait que notre plan est infini et récouvre l'intégralité de l'espace.

On va donc devoir modifier un chouia notre code pour le faire apparaître de nouveau.

On va conditionner l'application de notre matériel si et seulement si la distance de l'objet n'est pas supérieur à notre distance d'affichage.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    ...

    // On applique l'algorithme de raymarching à ce pixel
    Data data = rayMarch(eye, rayDirector);
    
    vec3 col = vec3(0);

    // le matériel est appliqué seulement si l'objet n'est pas trop loin
    if( data.d < MAX_DISTANCE) {
        // On récupère le matériel
        col = material(data.m);
    }

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui nous donne:

On a bien le sol vert qui découpe du ciel noir, mais il y a une sorte d'aréole verte autour du demi-cercle rouge.

On peut d'ailleurs amplifier le phénomène en diminuant le nombre d'itérations de notre raymarcher.

#define MAX_ITERATIONS 20

Cela est dû au fait que le raymarcher n'atteint pas réellement la surface de l'objet du fait du faible nombre d'itérations. Ce qui conduit à des erreurs d'appréciation des distances et donc des problème d'attribution de matériel.

Pour avoir quelque chose de convenable on va au contraire augmenter ce nombre d'itérations.

#define MAX_ITERATIONS 200

Et voilà on a un ciel !! 🥳

Bon il est noir mais c'est temporaire on va le rendre bien plus beau par la suite !

Le code.

Les normales

Une partie essentielle d'un rendu réaliste du scène 3D est d'être dans la capacité de déterminer les variations géométriques de la surface que tente de rendre.

Une normal est un vecteur unitaire qui donne une indication sur la direction de l'extérieure de la surface.

crédit de l'image

Chacun des vecteurs de l'image partent de la surface selon une certaine direction.

Le but est donc de déterminer la direction de ce vecteur sur l'ensemble de la scène.

Pour ceux qui s'en rappellent on va utiliser le même principe que lorsque l'on cherche la pente d'une courbe, autrement dit sa dérivée.

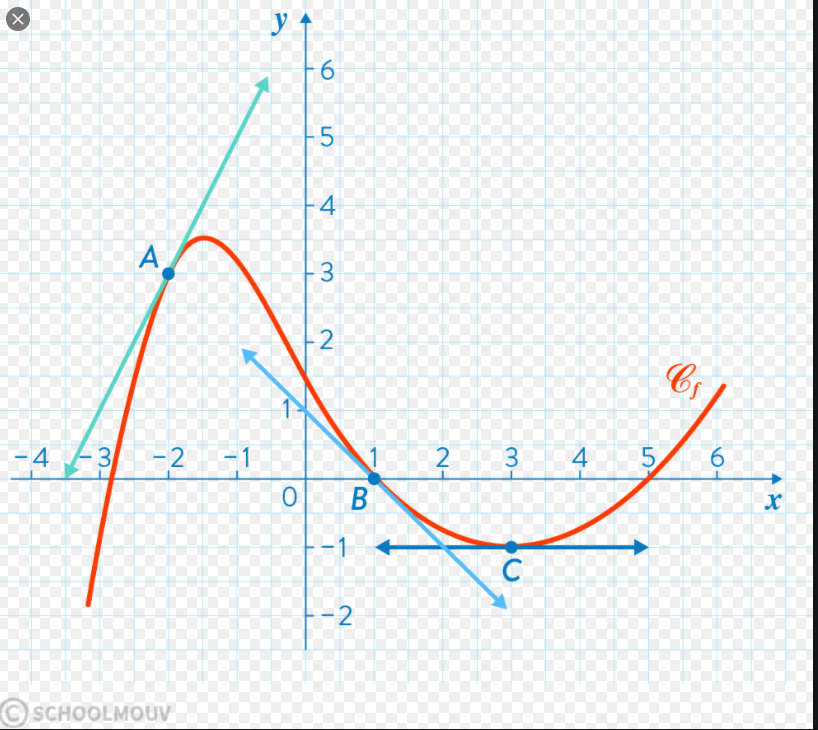
Calculer une dérivée revient à caculer une application en un point, se déplacer d'une petite distance recalculer l'application en ce nouveau point. Et faire la la différence entre ces deux résultat.

Dans le cadre d'une f(x), en 1D. dx = f(x + h) - f(x) où h est le plus petit possible.

On va généraliser la chose dans la 3ème dimension.

Et caluler notre dérivé dans les 3 dimensions.

Notre application dans le cadre du calcul de la normale à une surface en un point est tout simplement notre fonction scene appliquée en un point.

Pour se déplacer dans les x, y et z. On va définir h suffisamment petit permettant de nous déplacer sur la surface.

Nous sommes surtout intéressés par la direction du vecteur et non pas sa norme.

On normalise donc le vecteur composé des dx, dy, dz calculés.

/**
* Calcul le vector normal d'un point de la scène
* point : Point de la scène qui doit être calculé
*/
vec3 normal(vec3 point) {
    float dp = scene(point).d;
    
    vec2 eps = vec2(0.001, 0);
    
    float dx = scene(point + eps.xyy).d - dp;
    float dy = scene(point + eps.yxy).d - dp;
    float dz = scene(point + eps.yyx).d - dp;
    
    return normalize(vec3(dx, dy, dz));
}

et modifie notre fonction d'affichage pour montrer le champ des normal:

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    ...

    vec3 col = vec3(0);

    // le matériel est appliqué seulement si l'object n'est pas trop loin
    if( data.d < MAX_DISTANCE) {
        
        // On recalcule le point par rapport à la distance trouvée lors du calcul de raymarch
        vec3 point = eye + rayDirector * data.d;
    
        // On récupère le matériel
        col = normal(point);
    }

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui nous permet d'afficher cette image:

Si on analyse un peu cette image, on peut tracer les normales que j'ai dessiné ici en violet.

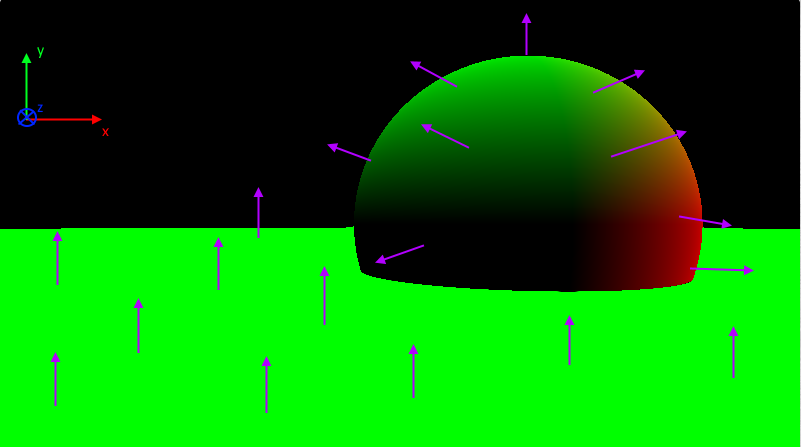
Plus une surface est rouge plus son vecteur normal est orienté dans l'axe des x.

Plus une surface est verte plus son vecteur normal est orienté dans l'axe des y.

Il n'y a pas de bleu car dès que l'on quitte la surface on n'affiche pas de couleur.

Les zones en noir correspondent à des composantes négatives, en effet une composante de couleur est négative elle ramenée à 0.

On remarque aussi que le sol est entièrement vert, c'est du au fait qu'il est entièrerement horizontal et donc sa normal est purement vertical et donc de valeur (0, 1, 0).

Le code

Et la lumière fut ! 🌞

Maintenant que l'on a nos normales en chaque point de notre surface on va pouvoir calculer la contribution d'une source lumineuse dans notre rendu de scène.

Pour cela nous allons faire appel à loi de Snell-Descartes sur l'incidence de la lumière réfléchi.

Ce que l'on désire c'est connaître l'intensité lumineuse reçu en chaque point de la scène.

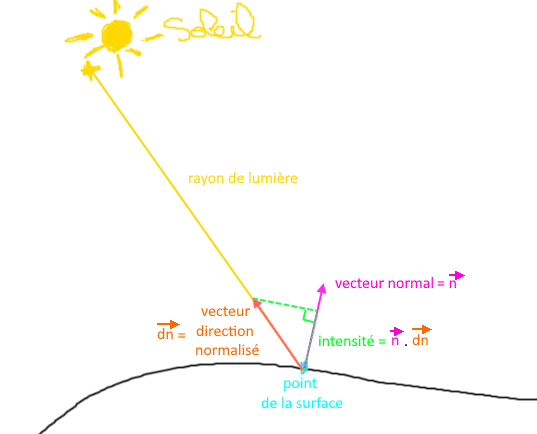
On trace un rayon de lumière entre le point de la surface qui doit être calculé et la source lumineuse.

On normalise ce vecteur.

Puis on réalise le produit scalaire entre ce vecteur direction et la normale à la surface en ce point.

/**
* Calcul l'intensité lumineuse renvoyée par la scène en un point à l'oeil
* point         : Point de la scène qui doit être calculé
* normal        : Vecteur normal à la surface au point calculé
* lightPosition : Position de la source de lumière dans l'espace
*/
float lighting(vec3 point, vec3 normal, vec3 lightPosition) {
    
    // On calcule le vecteur de la direction de la lumière
    vec3 lightDirection = lightPosition - point;
    
    // On normalise ce vecteur direction
    vec3 lightNormal = normalize(lightDirection);
    
    // Puis l'intensité lumineuse
    return dot(lightNormal, normal);
}

Puis on modifie la fonction d'affichage pour montrer la contribution de la lumière dans la scène.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    ...
    
    vec3 col = vec3(0);

    // le matériel est appliqué seulement si l'object n'est pas trop loin
    if( data.d < MAX_DISTANCE) {
        
        // On recalcule le point par rapport à la distance trouvée lors du calcul de raymarch
        vec3 point = eye + rayDirector * data.d;
    
        // On récupère le matériel
        vec3 normalVector = normal(point);
        
        // On calcule la lumière en un point de la scène
        float lightIntensity = lighting(point, normalVector, lightPosition);
        
        // Intensité lumineuse en niveau de gris
        col = vec3(lightIntensity);
    }

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui nous donne:

Plus la surface est blanche plus la normale est alignée avec la source de lumière.

Le code

On va maintenant rendre notre scène en prenant en compte le matériel de la surface ainsi que la contribution lumineuse.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    ...

    // le matériel est appliqué seulement si l'object n'est pas trop loin
    if( data.d < MAX_DISTANCE) {
        
        // On recalcule le point par rapport à la distance trouvée lors du calcul de raymarch
        vec3 point = eye + rayDirector * data.d;
    
        // On récupère le matériel
        vec3 normalVector = normal(point);
        
        // On calcule la lumière en un point de la scène
        float lightIntensity = lighting(point, normalVector, lightPosition);
        
        // On pondère le rendu du matériel avec la contribution lumineuse
        col = material(data.m) * lightIntensity;
    }

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Et voici le résultat on a une jolie ombre réaliste pour le côté non exposé.

Le code

Ombre et lumière les faces d'une même pièce 🌛

Notre scène a bien des ombres mais aucune ombre portée.

Donnons à notre scène un peu plus de réalisme.

Pour cela il faut se demander la chose suivante: Qu'est-ce qu'une ombre ?

La réponse évidente est une absence de lumière.

Mais qu'est ce qui provoque cette absence de lumière ? La réponse est souvent un obstacle entre l'objet 3D plongé dans l'ombre et la source de lumière.

Pour déterminer s'il y a un obstacle entre un point de notre scène et une source lumineuse on va appliquer l'algorithme de raymarching en utilisant comme paramètres:

le point de la scène que l'on désire déterminer être dans l'ombre ou non
le rayon directeur de la lumière calulé précédemment

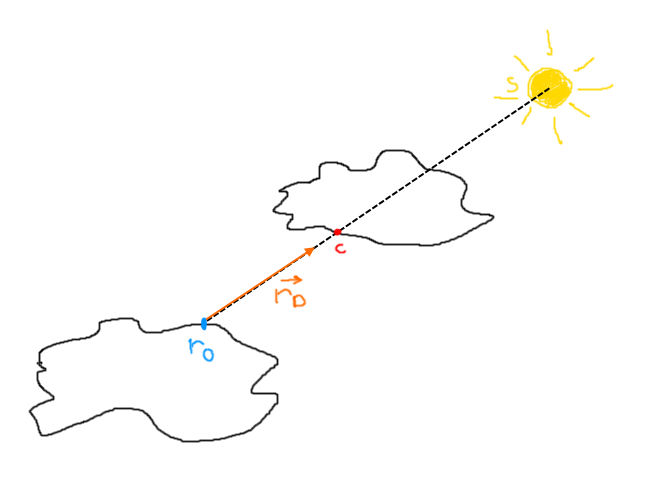
Le point rO de la scène est ici séparé de la source de lumière par un autre solide qui bloque la vue du point rO.

En appliquant l'algorithme de raymarching on va se retrouver au point C.

Si la distance rO -> C est inférieure à la distance r0 -> S.

Alors il y a un obstacle sur la route. L'intensité lumineuse en rO est donc nulle !

float lighting(vec3 point, vec3 normal, vec3 lightPosition) {
    
    // On calcule le vecteur de la direction de la lumière
    vec3 lightDirection = lightPosition - point;
    
    // On normalise ce vecteur direction
    vec3 lightNormal = normalize(lightDirection);
    
    // On caclule la distance qui sépare notre point de 
    Data data = rayMarch(point, lightNormal);
    
    // Si la distance calculé est inférieure à la longueur du rayon 
    // alors l'intensité lumineuse est nulle
    if (data.d < length(lightDirection)) {
        return 0.0;
    }
    
    // On calcule l'intensité lumineuse via le produit scalaire des deux vecteurs
    return dot(lightNormal, normal);
}

Oups! c'est pas trop ce qu'on voulait 😠

Alors qu'est ce qui se passe ?

Et bien on calcule le raymarching d'un point qui est lui même sur une surface de notre scène, donc toutes les distances calculées sont nulles !!

Pour corriger ce problème on va "décoller" notre point de calcul en se déplaçant très légèrement dans la direction de la normal à notre surface.

Data data = rayMarch(point + normal*0.01, lightNormal);

Et finalment on atteint le résultat escompté 😁

Et on peut amplifier la chose avec une lumière plus rasante.

// Source de lumière
vec3 lightPosition = vec3(3.0, 2.5, 0);

Le code

Correction colorimétrique

Tout capteur a ses défaut et l'oeil ne fait pas exception.

Le sujet est passionnant et je vous redirige vers cet article pour en savoir plus.

Ce qui est à retenir c'est ce tableau-ci:

La première ligne du tableau représente ce que l'on devrait voir avec un capteur linéaire et donc oeil parfait.

La seconde ce qu'un oeil distingue réellement. Il a tendance a mieux distinguer les hautes intensités lumineuses et être moins performant dans des conditions de plus faible luminostité.

Si on représente c'est valeurs sous la forme d'un graphique:

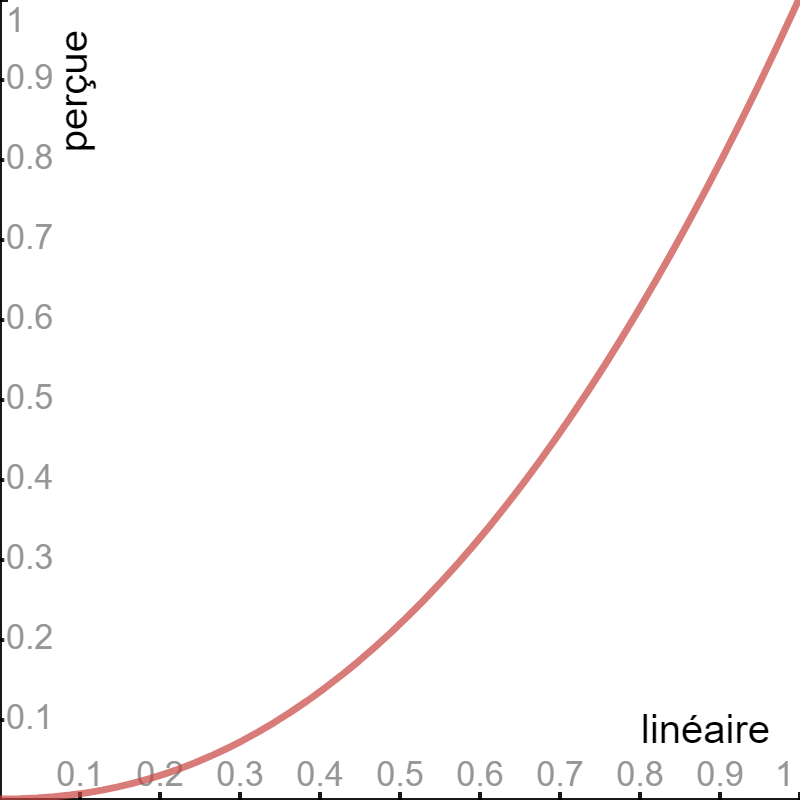
Le but va être alors de corriger ce manque précision dans les noirs pour rendre plus réelle notre rendu des couleurs.

On appelle ce coefficient d'erreur dans la colorimétrie le gamma de l'image. Que l'on note γ

Les données nous donne une valeur de γ de 2.2.

La courbe ainsi tracée à pour formule x^γ.

Pour revenir à une dynamique de constraste linénaire on va réaliser son symétrique par rapport l'axe f(x) = x, autrement dit f(x) = x ^ (1/γ)

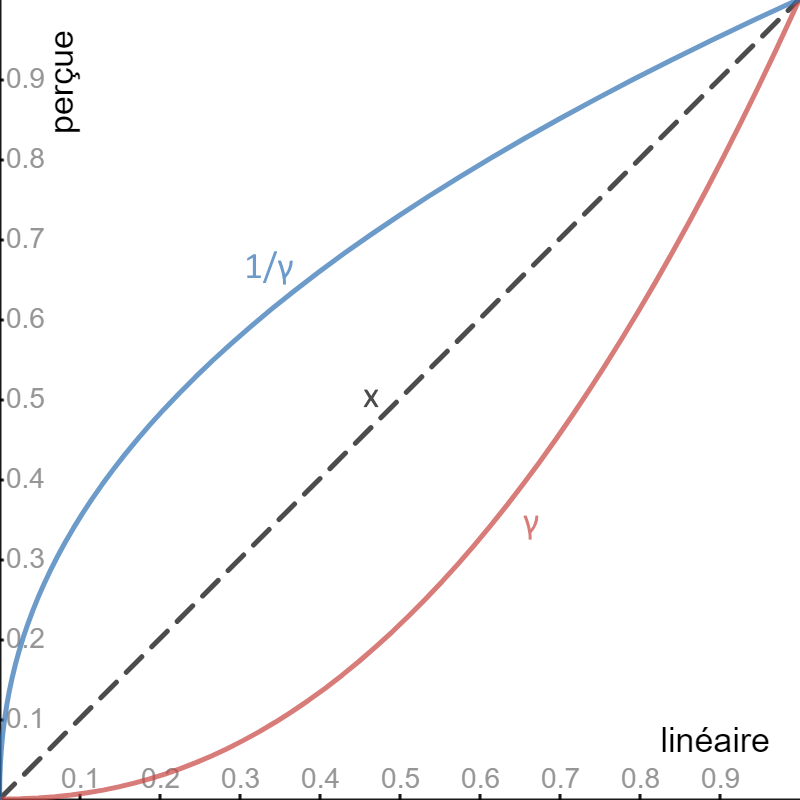
Bon maintenant que l'on a la théorie place à la pratique!

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    ...

    // Définition du gamma de l'image
    float gamma = 2.2;

    // On applique la correction du gamma de chaque de couleur du pixel
    col = pow(col, vec3(1./gamma));

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui nous donne ce résultat:

Comme toujours le code.

De meilleures couleurs

On a des couleurs, de la lumière des ombres portées et même une correction du gamma de notre image.

Mais qu'est ce que nos couleurs sont moches ! 🤢

On va d'abord un peu redéfinir notre dictionnaire de matériaux.

#define MATERIAL_SPHERE 1  
#define MATERIAL_FLOOR  2
#define MATERIAL_SKY    3

Ensuite il nous faut une palette de couleur cohérente. J'ai découvert très récemment le site coolors qui m'en fourni une.

Le petit soucis c'est que notre définition des couleurs de pixel est un peu spéciale.

En effet les composante de couleur vont de 0 à 1 dans notre système et de 0 à 255 sur coolors.

Le deuxième soucis est qu'ils ne prennent pas en compte les aberrations dûes au gamma de l'image.

si on se contente d'écrire:

vec3 material(int index) {

    vec3 material;

    switch(index) {
        case MATERIAL_SPHERE:
            material = vec3(89, 66, 54);
            break;
        case MATERIAL_FLOOR:
            material = vec3(255, 186, 73);
            break;
        case MATERIAL_SKY:
            material = vec3(10, 157, 255);
            break;
        default:
            material = vec3(0);
    }
    
  
    return material/255.;
        
}

On va obtenir des couleur qui sont un peu plus fades. Qui sont très belle au demeurant :)

Si on veut exactement les couleurs que l'on a dans la palette choisie, il va falloir opérer à des ajustements.

J'ai écrit un petit script qui permet de "corriger" les couleurs.

En remplaçant les valeurs trouvée.

/**
* Renvoie le matériel associé à l'index ou du noir si l'index est inconnu
* m : index du matériel
*/
vec3 material(int index) {

    vec3 material;

    switch(index) {
        case MATERIAL_SPHERE:
            material = vec3(98.69, 51.12, 32.88);
            break;
        case MATERIAL_FLOOR:
            material = vec3(1000.00, 499.51, 63.81);
            break;
        case MATERIAL_SKY:
            material = vec3(0.80, 344.03, 1000.00);
            break;
        default:
            material = vec3(0);
    }
    
  
    return material / 1000.;
        
}

On obtient:

Et c'est bien plus beau 😎

Le code associé au chapitre.

Un ciel légèrement plus réaliste

Dans la vraie vie le ciel n'est jamais bleu uni comme cela, ça se rapproche plutôt d'un dégradé comme celui ci:

On va donc essayer de mettre en place ceci pour notre scène.

Tout d'abord, l'on va définir non pas une couleur de ciel, mais deux, une pour la couleur sombre du dégradé et une deuxième pour la couleur claire du dégradé.

#define MATERIAL_SPHERE      1  
#define MATERIAL_FLOOR       2
#define MATERIAL_SKY_LIGHT   3
#define MATERIAL_SKY_DARK    4

Ensuite nous allons utiliser une fonction d'interpolation linéaire appelée mix.

Elle prend 3 paramètres:

le vecteur x : couleur claire du dégradé
le vecteur y : couleur sombre du dégradé
le coefficient a : coefficient à appliquer

Et renvoie un vecteur de sortie s.

La formule appliquée sur chaque composante des vecteurs est s = (1- a) * x + a * y

Pour générer notre dégradé qui va de notre couleur claire vers notre couleur sombre, on va devoir définir notre coefficient en fonction des uv.y de notre image.

Pour rappel:

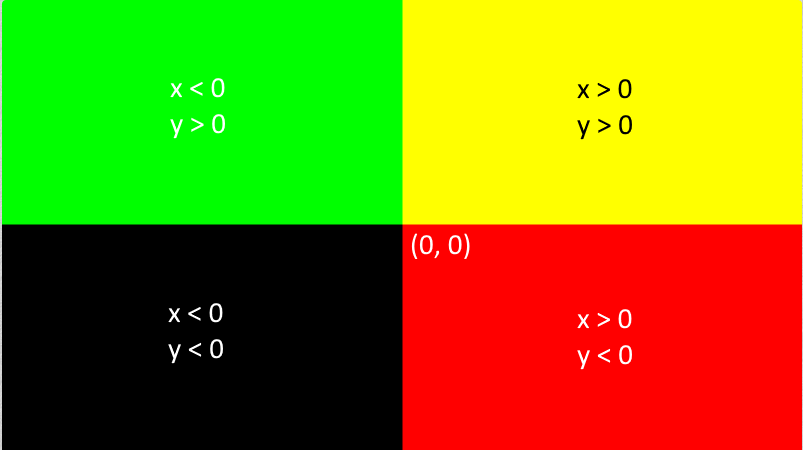
Le centre de l'image à une valeur d'uv de (0,0) et le coin supérieur droit(1, 1).

Nous allons donner à notre gradient cette courbe de coefficient:

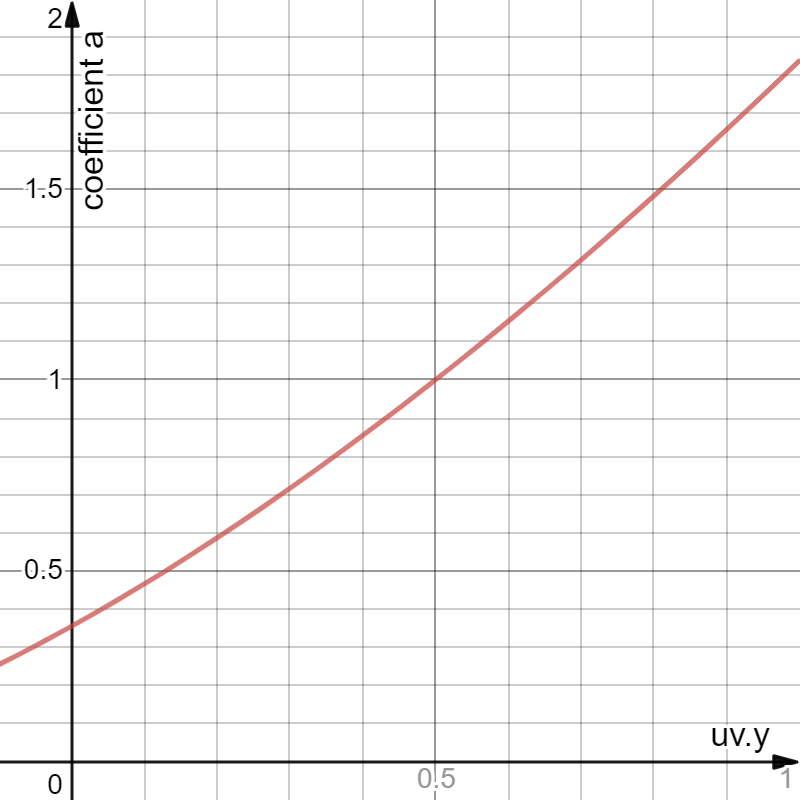
La formule est a(y) = (y + 0.5) ^ 1.5

Et maintenant le code!

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Calcule des UV de l'écran
    vec2 uv = (fragCoord- 0.5*iResolution.xy) / iResolution.y;
    
    ...
    
    // ciel
    vec3 skyColDark  = material(MATERIAL_SKY_DARK);
    vec3 skyColLight = material(MATERIAL_SKY_LIGHT);
    
    vec3 col = mix(skyColLight, skyColDark, pow(uv.y + 0.5, 1.5));

    ....

    // Output to screen
    fragColor = vec4(col, 1.0);
}

Ce qui donne:

Beaucoup mieux! 😃

Il reste une petite chose à traiter. La lumière est réfléchi par les couches de l'atmosphère et redirigé vers le sol.

Dans un but de simplification on va considéré que cette lumière venant du ciel est purement vertical (ce qui n'est évidemment pas vrai).

On va définir une composant de couleur supplémentaire que l'on va additionner au lumière calculées.

// Définition de la couleur venant du ciel
vec3 ambiantSky = normalVector.y * skyColLight;

// On pondère le rendu du matériel avec la contribution lumineuse
col = material(data.m) * (lightIntensity + ambiantSky);

Et voici le rendu finale de notre scène!!

Le code.

Conclusion

On est passé de

Quelle aventure cette article 😁. On a appris à:

appliquer un matériel sur un objet de notre scène.
calculer les lumières de manière réaliste
calculer les ombres associées
gérer la colorimétrie et le gamma de notre image
et enfin faire un ciel digne de ce nom !

Dans la prochaine partie on verra comment implémenter une caméra dans ce monde 3D un peu plus perfectionnée que maintenant.

Je vous remercie de votre lecture et je vous dis à la prochaine pour de nouveaux articles, sur les shaders ou un autre sujet. 💗

Auteur: Akanoa

Je découvre, j'apprends, je comprends et j'explique ce que j'ai compris dans ce blog.

Ce travail est sous licence CC BY-NC-SA 4.0.